基础课
DFS
深度优先搜索

模板
int dfs(int u)
{
st[u] = true; // st[u] 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j);
}
}原题链接:排列数字
#include<iostream>
using namespace std;
const int N = 10;
int n; //存储层数
int path[N]; //存储当前排列
bool st[N]; //存储状态数组,为true说明该位置有数,为false说明该位置无数,初始化后为false
void dfs(int u)
{
if(u == n) //达到最底层的时候即输出当前排列
{
for (int i=0;i < n;i ++) printf("%d ",path[i]);
puts("");
return;
}
for (int i = 1; i <= n;i ++ ) //每一次深搜都要进行一次遍历
if (!st[i]) //对于每一个为true的数,只寻找后面为false的数,如1为true,2、3为false,则队列变为12,13
{
path[u] = i; //为当前深搜排列进行赋值
st[i] = true; //将搜到的数置为true
dfs(u+1); //下一层进行深度搜索
st[i] = false; //,若下一层到了底层,则回溯节点
}
}
int main()
{
cin >> n;
dfs(0); //从第0层开始搜索
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 10;
public static int n; // 层数
public static int path[] = new int[N]; // 当前排列
public static boolean st[] = new boolean[N];
public static void dfs(int u) {
if (u == n) {
for (int i = 0; i < n; i++)
out.print(path[i] + " ");
out.println();
return;
}
for (int i = 1; i <= n; i++) {
if (!st[i]) {
path[u] = i;
st[i] = true;
dfs(u + 1);
st[i] = false;
}
}
}
public static void main(String[] args) throws Exception {
n = nextInt();
dfs(0);
out.flush();
}
}#include<iostream>
#include<algorithm>
using namespace std;
const int N = 10, M = 2*N;
bool col[N], dg[M], udg[M];
char path[N];
int n;
char g[N][N];
void dfs(int u){
if(u == n){
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0; j <n ; j ++ ){
cout << g[i][j] ;
}
cout << endl;
}
cout << endl;
return ;
}
for(int i = 0 ; i < n ; i ++ ){
if(!col[i] && !dg[u + i] && !udg[u - i + n]){
g[u][i] = 'Q';
col[i] = dg[u+i] = udg[u-i+n] = true;
dfs(u + 1);
col[i] = dg[u+i] = udg[u-i+n] = false;
g[u][i] = '.';
}
}
}
int main(){
cin >> n;
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
g[i][j] = '.';
}
}
dfs(0);
return 0;
}BFS
能走最短路径
只有边权都是1时,才能用BFS求最短路径


注意这里的方向dx[4] = {-1, 0, 1, 0}, dy[4] = {0,1,0,-1},分别是上、右、下、左

模板:
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍 历过
q.push(j);
}
}
}原题链接:https://www.acwing.com/problem/content/846/
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int,int> PII;
const int N = 110;
int n,m;
int g[N][N]; //存储原数据
int d[N][N]; //存储路径
PII q[N*N]; //模拟队列
int bfs()
{
int hh = 0, tt = 0; //hh为队头,tt为队尾
q[0] = {0,0};//模拟队列
memset(d, -1 , sizeof d);
int dx[4] = {-1,0,1,0} , dy[4] = {0,-1,0,1};//用(-1,0),(0,1),(1,0),(0,-1)模拟点的上下移动
d[0][0] = 0;
while(hh <= tt)
{
auto t = q[hh++];//取出队头
for(int i = 0 ; i < 4 ; i ++ )//扩展队列
{
int x = t.first + dx[i], y = t.second + dy[i];
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;
q[++tt] = {x,y};
}
}
}
return d[n-1][m-1];
}
int main()
{
cin >> n >> m;
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < m ; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 110;
int n,m;
int g[N][N];
int d[N][N];
queue<PII> q;
int bfs()
{
memset(d,-1,sizeof d);
q.push({0,0});
d[0][0] = 0;
int dx[4] = {-1,0,1,0} , dy[4] = {0,-1,0,1};
while(!q.empty())
{
auto t = q.front();
q.pop();
for(int i = 0 ; i < 4 ; i ++ )
{
int x = t.first + dx[i] , y = t.second + dy[i];
if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1)
{
q.push({x,y});
d[x][y] = d[t.first][t.second] + 1;
}
}
}
return d[n-1][m-1];
}
int main()
{
cin >> n >> m;
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < m ; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 110;
public static int n, m;
public static int g[][] = new int[N][N];
public static int d[][] = new int[N][N];
public static Queue<Pairs> q = new LinkedList<Pairs>();
public static int bfs() {
for(int i = 0; i < n ; i ++ ){
Arrays.fill(d[i],-1);
}
q.add(new Pairs(0, 0));
d[0][0] = 0;
int dx[] = { -1, 0, 1, 0 }, dy[] = { 0, 1, 0, -1 };
while (!q.isEmpty()) {
Pairs p = q.element();
q.remove();
for (int i = 0; i < 4; i++) {
int x = p.first + dx[i], y = p.second + dy[i];
if (x >= 0 && x < n && y < m && y >= 0 && g[x][y] == 0 && d[x][y] == -1) {
q.add(new Pairs(x, y));
d[x][y] = d[p.first][p.second] + 1;
}
}
}
return d[n - 1][m - 1];
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
g[i][j] = nextInt();
}
}
int res = bfs();
out.print(res);
out.flush();
}
}
class Pairs {
int first;
int second;
public Pairs(int first, int second) {
this.first = first;
this.second = second;
}
}#include<iostream>
#include<queue>
#include<unordered_map>
#include<cstring>
using namespace std;
int bfs(string start){
string end = "12345678x";
int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
queue<string> q;
unordered_map<string,int> d;
q.push(start);
d[start] = 0;
while(!q.empty()){
string s = q.front();
q.pop();
int dis = d[s];
if(s == end) return dis;
int k = s.find('x');
int x = k / 3;
int y = k % 3;
for(int i = 0 ; i < 4 ; i ++ ){
int a = x + dx[i], b = y + dy[i];
if(a >= 0 && a < 3 && b >= 0 && b < 3){
swap(s[k], s[a * 3 + b]);
if(!d.count(s)){
d[s] = dis + 1;
q.push(s);
}
swap(s[k], s[a * 3 + b]);
}
}
}
if(d[end] == 0) return -1;
return d[end];
}
int main(){
string start;
for(int i = 0 ; i < 9 ; i ++ ){
char c;
cin >> c;
start += c;
}
cout << bfs(start) << endl;
return 0;
}树与图的深度优先遍历
原题链接:树的重心
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5+10, M = 2*N;
int n;
int idx,e[M],ne[M],h[N];
bool st[N];
int ans = N;
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++ ;
}
int dfs(int u){
st[u] = true;
int size = 0, sum = 1;
for(int i = h[u]; i != -1 ; i = ne[i]){
int j = e[i];
if(!st[j]) {
int s = dfs(j);
size = max(size, s); //记录最大联通子图的节点数
sum += s; //以j为根的树的节点数
}
}
size = max(size , n - sum);
ans = min(size, ans);
return sum;
}
int main(){
memset(h,-1,sizeof h);
cin >> n;
for(int i = 0 ; i < n - 1 ; i ++ ){
int a,b;
cin >> a >> b;
add(a,b);
add(b,a);
}
dfs(1);
cout << ans <<endl;
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 100010, M = 2 * N;
public static int n, idx, res = N;
public static int h[] = new int[N];
public static int e[] = new int[M];
public static int ne[] = new int[M];
public static boolean st[] = new boolean[N];
public static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
public static int dfs(int u) {
st[u] = true;
int size = 0, sum = 1;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (st[j])
continue;
int s = dfs(j);
size = Math.max(size, s);
sum += s;
}
size = Math.max(size, n - sum);
res = Math.min(size, res);
return sum;
}
public static void main(String[] args) throws Exception {
n = nextInt();
Arrays.fill(h, -1);
for (int i = 0; i < n - 1; i++) {
int a, b;
a = nextInt();
b = nextInt();
add(a, b);
add(b, a);
}
dfs(1);
out.print(res);
out.flush();
}
}
树与图的广度优先遍历
原题链接:图中点的层次
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e5 +10;
int n,m;
int idx,e[N],ne[N],h[N],d[N];
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++ ;
}
int bfs(){
memset(d,-1,sizeof d);
queue<int> q;
q.push(1);
d[1] = 0;
while(!q.empty()){
int t = q.front();
q.pop();
for(int i = h[t] ; i != -1; i = ne[i]){
int j = e[i];
if(d[j] == -1){
d[j] = d[t] + 1;
q.push(j);
}
}
}
return d[n];
}
int main(){
memset(h,-1,sizeof h);
cin >> n >> m;
for(int i = 0 ; i < m ; i ++ ){
int a,b;
cin >> a >> b;
add(a,b);
}
cout << bfs() << endl;
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 100010;
public static int n, m, idx;
public static int h[] = new int[N];
public static int e[] = new int[N];
public static int ne[] = new int[N];
public static int d[] = new int[N];
public static Queue<Integer> q = new LinkedList<Integer>();
public static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
public static int bfs() {
Arrays.fill(d, -1);
d[1] = 0;
q.add(1);
while (!q.isEmpty()) {
int t = q.element();
q.remove();
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] == -1) {
d[j] = d[t] + 1;
q.add(j);
}
}
}
return d[n];
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
Arrays.fill(h, -1);
for (int i = 0; i < m; i++) {
int a, b;
a = nextInt();
b = nextInt();
add(a, b);
}
int res = bfs();
out.print(res);
out.flush();
}
}
拓扑序列

模板:
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点,e[k]存储该边的目的节点,ne[N]存储所有的边,
int h[N], e[N], ne[N], idx;
// 添加一条边a->b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0;
memset(h, -1, sizeof h);
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度,即存储所有入度为0的点
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i]) //遍历该点的所有边
{
int j = e[i];
if (-- d[j] == 0)
q[ ++ tt] = j;
//遍历每个目的节点,若度数减1后为0,则将该点插入到拓扑队列中
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;
}public static int idx, cnt;
public static int h[] = new int[N];
public static int e[] = new int[N];
public static int ne[] = new int[N];
public static int d[] = new int[N];
public static int ans[] = new int[N];
public static Queue<Integer> q = new LinkedList<Integer>();
public static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
public static boolean topsort() {
for(int i = 1; i <= n; i++ ) {
if(d[i] == 0) {
q.add(i);
}
}
while(!q.isEmpty()) {
int t = q.element();
q.remove();
ans[cnt++] = t;
for(int i = h[t] ; i != -1; i= ne[i]) {
int j = e[i];
d[j] -- ;
if(d[j] == 0) {
q.add(j);
}
}
}
return cnt == n;
}原题链接:有向图的拓扑序列
#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010;
int idx,h[N],e[N],ne[N];
int n,m;
int q[N],d[N];
void add(int a,int b)
{
e[idx] = b , ne[idx] = h[a], h[a] = idx ++ ;
}
bool topsort()
{
int tt = -1 , hh = 0 ;
for(int i = 1 ; i <= n ; i ++ )
if(!d[i]) q[++tt] = i;
while(hh<=tt)
{
int t = q[hh++];
for(int i = h[t] ; i != -1 ; i = ne[i])
{
int j = e[i];
d[j] -- ;
if(!d[j]) q[++tt] = j;
}
}
return tt == n - 1;
}
int main()
{
cin >> n >> m;
memset(h,-1,sizeof h);
for(int i = 0 ; i < m ; i ++ )
{
int a,b;
cin >> a >> b;
add(a,b);
d[b]++;
}
if(topsort())
{
for(int i = 0 ; i < n ; i ++ ) printf("%d ",q[i]);
puts("");
}
else puts("-1");
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 100010;
public static int n, m, idx, cnt;
public static int h[] = new int[N];
public static int e[] = new int[N];
public static int ne[] = new int[N];
public static int d[] = new int[N];
public static int ans[] = new int[N];
public static Queue<Integer> q = new LinkedList<Integer>();
public static void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
public static boolean topsort() {
for(int i = 1; i <= n; i++ ) {
if(d[i] == 0) {
q.add(i);
}
}
while(!q.isEmpty()) {
int t = q.element();
q.remove();
ans[cnt++] = t;
for(int i = h[t] ; i != -1; i= ne[i]) {
int j = e[i];
d[j] -- ;
if(d[j] == 0) {
q.add(j);
}
}
}
return cnt == n;
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
Arrays.fill(h, -1);
for (int i = 0; i < m ; i++) {
int a, b;
a = nextInt();
b = nextInt();
add(a, b);
d[b] ++ ;
}
if(topsort()) {
for(int i = 0 ; i < cnt ; i ++ ) out.print(ans[i] + " ");
out.println();
}else {
out.print(-1);
}
out.flush();
}
}
Dijkstra
朴素Dijkstra

稀疏图:邻接矩阵 稠密图:邻接表
模板:
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
原题链接:https://www.acwing.com/problem/content/851/
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510;
int n ,m ;
int g[N][N];
bool st[N];
int d[N];
int dijstra()
{
memset(d, 0x3f, sizeof d);
d[1] = 0;
for(int i = 0 ; i < n ; i ++ )
{
int t = -1;
for(int j = 1 ; j <= n ; j ++ )
{
if(!st[j] && (t == -1 || d[t] > d[j]))
t = j ;
}
for(int j = 1 ; j <= n ; j ++ )
{
d[j] = min(d[j], d[t] + g[t][j]);
}
st[t] = true;
}
if(d[n] == 0x3f3f3f3f) return -1;
return d[n];
}
int main()
{
scanf("%d%d",&n,&m) ;
memset(g,0x3f,sizeof g);
for(int i = 0 ; i < m ; i ++ ){
int x, y, z;
scanf("%d%d%d",&x,&y,&z);
g[x][y] = min(g[x][y], z);
}
int t = dijstra();
printf("%d",t);
return 0;
}堆优化Dijkstra
模板
typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 150010;
int n,m;
int idx,h[N],e[N],ne[N],w[N];
int d[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx] = b , w[idx] = c , ne[idx] = h[a], h[a] = idx ++ ;
}
int dijstra()
{
memset(d, 0x3f , sizeof d);
d[1] = 0;
priority_queue<PII,vector<PII>,greater<PII>> heap; //小根堆,按first从小到大
heap.push({0,1});
while(heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second,distance = t.first; //first是距离,second是枚举的点
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1 ; i = ne[i])
{
int j = e[i];
if(d[j] > distance + w[i])
{
d[j] = distance + w[i];
heap.push({d[j],j});
}
}
}
if(d[n] == 0x3f3f3f3f) return -1;
return d[n];
}
int main()
{
memset(h, -1 ,sizeof h);
scanf("%d%d",&n,&m);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int t = dijstra();
printf("%d",t);
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 150010;
public static int n, m, idx;
public static int h[] = new int[N];
public static int e[] = new int[N];
public static int ne[] = new int[N];
public static int w[] = new int[N];
public static int d[] = new int[N];
public static boolean st[] = new boolean[N];
public static void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
public static int dijsktra() {
Arrays.fill(d, 0x3f3f3f3f);
d[1] = 0;
PriorityQueue<Pairs> pq = new PriorityQueue<Pairs>();
pq.add(new Pairs(0, 1));
while (!pq.isEmpty()) {
Pairs t = pq.element();
pq.remove();
int ver = t.second, distance = t.first;
if (st[ver])
continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] > distance + w[i]) {
d[j] = distance + w[i];
pq.add(new Pairs(d[j], j));
}
}
}
if (d[n] == 0x3f3f3f3f)
return -1;
return d[n];
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
Arrays.fill(h, -1);
for (int i = 0; i < m; i++) {
int a, b, c;
a = nextInt();
b = nextInt();
c = nextInt();
add(a, b, c);
}
int t = dijsktra();
out.print(t);
out.flush();
}
}
class Pairs implements Comparable<Pairs> {
int first; // 距离
int second; // 枚举的点
public Pairs(int first, int second) {
this.first = first;
this.second = second;
}
@Override
public int compareTo(Pairs p) {
if (this.first != p.first) {
return this.first - p.first;
} else {
return this.second - p.second;
}
}
}
bellman-ford
不能存在负权回路

模板:
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在负权回路。
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}原题链接:有边数限制的最短路
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int M = 10010,N = 510;
int n,m,k;
struct Edge{
int a,b,w;
}edges[M];
int d[N],backup[N];
//backup存在的意义是进行备份,防止dist数组出现串联更新的结果,简单来说就是在一次迭代时,前面的dist值发生变化,则后面的dist值会使用前面变化后的值,因此我们在每次迭代后都需要进行备份,从而使dist改变时是与备份的值相比较
bool flag; //判断答案是否正好为-1
int bellman_ford()
{
memset(d,0x3f,sizeof d);
d[1] = 0;
for(int i = 0 ; i < k ; i ++ )
{
memcpy(backup, d, sizeof d);
for(int j = 0 ; j < m ; j ++ )
{
int a = edges[j].a, b = edges[j].b , w = edges[j].w;
d[b] = min(d[b],backup[a]+w);
}
}
if(d[n] > 0x3f3f3f3f / 2)
{
flag = true;
return -1;
}
return d[n];
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(int i = 0 ; i < m ; i ++ )
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
edges[i] = {a,b,w};
}
int t = bellman_ford();
if(flag && t == -1) puts("impossible");
else printf("%d",t);
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 510, M = 10010;
public static int n, m, k;// n表示点数,m表示边数
public static int d[] = new int[N]; // d[x]存储1到x的最短路距离
public static int backup[] = new int[N];
public static Edge edges[] = new Edge[M];
public static boolean flag;
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
public static int bellman_ford() {
Arrays.fill(d, 0x3f3f3f3f);
d[1] = 0;
for (int i = 0; i < k; i++) {
backup = Arrays.copyOf(d, d.length);
for (int j = 0; j < m; j++) {
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
d[b] = Math.min(d[b], backup[a] + w);
}
}
if (d[n] > 0x3f3f3f3f / 2) {
flag = true;
return -1;
}
return d[n];
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
k = nextInt();
for (int i = 0; i < m; i++) {
int a, b, w;
a = nextInt();
b = nextInt();
w = nextInt();
edges[i] = new Edge(a, b, w);
}
int t = bellman_ford();
if (flag && t == -1)
out.println("impossible");
else
out.print(t);
out.flush();
}
}
class Edge {
int a, b, w;
public Edge(int a, int b, int w) {
this.a = a;
this.b = b;
this.w = w;
}
}spfa

模板:
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}原题链接:spfa求最短路
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 100010;
int n,m;
int h[N], w[N], e[N], ne[N], idx;
int d[N];
bool st[N],flag; //st数组存储的是该点是否在队列当中
void add(int a,int b,int c)
{
e[idx] = b, w[idx] = c , ne[idx] = h[a] , h[a] = idx ++;
}
int spfa()
{
memset(d, 0x3f, sizeof d);
d[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while(q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i = h[t] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(d[j] > d[t] + w[i])
{
d[j] = d[t] + w[i];
if(!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
if(d[n] > 0x3f3f3f3f/2){
flag = true;
return -1;
}
return d[n];
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int t = spfa();
if(flag && t == -1) puts("impossible");
else printf("%d",t);
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 100010;
public static int n, m, idx;
public static boolean flag;
public static int h[] = new int[N];
public static int w[] = new int[N];
public static int e[] = new int[N];
public static int ne[] = new int[N];
public static int d[] = new int[N];
public static boolean st[] = new boolean[N];
public static void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
public static int spfa() {
Arrays.fill(d, 0x3f3f3f3f);
d[1] = 0;
Queue<Integer> q = new LinkedList<Integer>();
q.add(1);
st[1] = true;
while (!q.isEmpty()) {
int t = q.element();
q.remove();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] > d[t] + w[i]) {
d[j] = d[t] + w[i];
if (!st[j]) {
q.add(j);
st[j] = true;
}
}
}
}
if (d[n] > 0x3f3f3f3f / 2) {
flag = true;
return -1;
}
return d[n];
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
Arrays.fill(h, -1);
for (int i = 0; i < m; i++) {
int a, b, c;
a = nextInt();
b = nextInt();
c = nextInt();
add(a, b, c);
}
int t = spfa();
if (flag && t == -1)
out.println("impossible");
else
out.print(t);
out.flush();
}
}
原题链接:spfa判断负环
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 100010;
int n,m;
int h[N], w[N], e[N], ne[N], idx;
int d[N],cnt[N];
bool st[N],flag;
void add(int a,int b,int c)
{
e[idx] = b, w[idx] = c , ne[idx] = h[a] , h[a] = idx ++;
}
int spfa()
{
//因为负环的存在,所以即使每个点距离虚拟原点距离为0,负权边的存在依然可以更新某个点为更小的负值
queue<int> q;
for(int i = 1 ; i <= n ; i++ )
{
st[i] = true;
q.push(i);
}
while(q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i = h[t] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(d[j] > d[t] + w[i])
{
d[j] = d[t] + w[i];
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n) return true;
if(!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
if(spfa()) puts("Yes");
else puts("No");
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 100010;
public static int n, m, idx;
public static boolean flag;
public static int h[] = new int[N];
public static int w[] = new int[N];
public static int e[] = new int[N];
public static int ne[] = new int[N];
public static int d[] = new int[N];
public static int cnt[] = new int[N];
public static boolean st[] = new boolean[N];
public static void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
public static boolean spfa() {
Queue<Integer> q = new LinkedList<Integer>();
for (int i = 1; i <= n; i++) {
st[i] = true;
q.add(i);
}
while (!q.isEmpty()) {
int t = q.element();
q.remove();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] > d[t] + w[i]) {
d[j] = d[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n)
return true;
if (!st[j]) {
q.add(j);
st[j] = true;
}
}
}
}
return false;
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
Arrays.fill(h, -1);
for (int i = 0; i < m; i++) {
int a, b, c;
a = nextInt();
b = nextInt();
c = nextInt();
add(a, b, c);
}
if (spfa())
out.print("Yes");
else
out.print("No");
out.flush();
}
}
Floyd
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
原题链接:https://www.acwing.com/problem/content/856/
#include<iostream>
#include<cstring>
using namespace std;
const int N = 210, INF = 1e9;
int n,m,Q;
int d[N][N];
void floyd()
{
for(int k = 1 ;k <= n ; k ++ )
{
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = 1 ; j <= n ; j ++ )
{
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&Q);
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = 1 ; j <= n ; j ++ )
{
if(i == j) d[i][i] = 0;
else d[i][j] = INF;
}
}
while(m--)
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
d[a][b] = min(d[a][b],w);
}
floyd();
while(Q--)
{
int a,b;
scanf("%d%d",&a,&b);
if(d[a][b] > INF/2) puts("impossible");
else printf("%d\n",d[a][b]);
}
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 210;
public static int n, m, Q, idx, INF = (int) 1e9;
public static int d[][] = new int[N][N];
public static void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
Q = nextInt();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j)
d[i][j] = 0;
else
d[i][j] = INF;
}
}
while (m-- > 0) {
int a, b, w;
a = nextInt();
b = nextInt();
w = nextInt();
d[a][b] = Math.min(d[a][b], w);
}
floyd();
while (Q-- > 0) {
int a, b;
a = nextInt();
b = nextInt();
if (d[a][b] > INF / 2)
out.println("impossible");
else
out.println(d[a][b] + " ");
}
out.flush();
}
}Prim

适用于稠密图
模板:
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF;
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
原题链接:Prim算法求最小生成树
#include<cstring>
#include<iostream>
using namespace std;
const int N = 510 , INF = 0x3f3f3f3f;
int g[N][N];
int n,m;
bool st[N];
int d[N];
int prim()
{
memset(d, 0x3f, sizeof d);
int res = 0;
for(int i = 0 ; i < n ; i ++ )
{
int t = -1;
for(int j = 1 ; j <= n ; j ++ )
{
if(!st[j] && (t == -1 || d[t] > d[j]))
t = j;
}
if(i && d[t] == INF) return INF;
if(i) res += d[t];
for(int j = 1; j <= n ; j ++ ) d[j] = min(d[j],g[t][j]);
st[t] = true;
}
return res;
}
int main()
{
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b] = g[b][a] = min(g[a][b],c);
}
int t = prim();
if(t == INF) puts("impossible");
else printf("%d",t);
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 510;
public static int n, m, INF = 0x3f3f3f3f;
public static int g[][] = new int[N][N];// 邻接矩阵,存储所有边
public static int d[] = new int[N];// 存储其他点到当前最小生成树的距离
public static boolean st[] = new boolean[N];// 存储每个点是否已经在生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
public static int Prim() {
Arrays.fill(d, 0x3f3f3f3f);
int res = 0;
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || d[t] > d[j]))
t = j;
}
if (i > 0 && d[t] == INF)
return INF;
if (i > 0)
res += d[t];
for (int j = 1; j <= n; j++)
d[j] = Math.min(d[j], g[t][j]);
st[t] = true;
}
return res;
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
for(int i = 1;i <= n ;i++){
Arrays.fill(g[i], 0x3f3f3f3f);
}
while (m-- > 0) {
int a, b, c;
a = nextInt();
b = nextInt();
c = nextInt();
g[a][b] = g[b][a] = Math.min(g[a][b], c);
}
int t = Prim();
if (t == INF)
out.print("impossible");
else
out.print(t + " ");
out.flush();
}
}
Kruskal

适用于稀疏图
模板:
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x) // 并查集核心操作
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}原题链接:https://www.acwing.com/problem/content/861/
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 200010;
int n,m;
int p[N];
struct Edge{
int a,b,w;
bool operator< (const Edge &W) const {
return w < W.w;
}
}edges[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 0 ; i < m ; i ++ )
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
edges[i] = {a,b,w};
}
sort(edges,edges+m);
for(int i = 1; i <= n ; i ++ ) p[i] = i;
int res = 0 , cnt = 0;
for(int i = 0; i < m ; i ++ )
{
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
a=find(a),b=find(b);
if(a != b)
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if(cnt < n - 1) puts("impossible");
else printf("%d",res);
return 0;
}import java.io.*;
import java.util.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws Exception {
in.nextToken();
return (int) in.nval;
}
public static int N = 200010, INF = 0x3f3f3f3f;
public static int n, m;
public static int p[] = new int[N];
public static Edge edges[] = new Edge[N];
public static int find(int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
public static int Kruskal() {
Arrays.sort(edges, 0, m);
for (int i = 1; i <= n; i++)
p[i] = i;
int res = 0, cnt = 0;
for (int i = 0; i < m; i++) {
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a);
b = find(b);
if (a != b) {
p[a] = b;
res += w;
cnt++;
}
}
if (cnt < n - 1)
return INF;
return res;
}
public static void main(String[] args) throws Exception {
n = nextInt();
m = nextInt();
for (int i = 0; i < m; i++) {
int a, b, w;
a = nextInt();
b = nextInt();
w = nextInt();
edges[i] = new Edge(a, b, w);
}
int res = Kruskal();
if (res == INF)
out.print("impossible");
else
out.print(res);
out.flush();
}
}
class Edge implements Comparable<Edge> {
int a, b, w;
public Edge(int a, int b, int w) {
this.a = a;
this.b = b;
this.w = w;
}
@Override
public int compareTo(Edge o) {
return this.w - o.w;
}
}
染色法判定二分图

一个图是二分图,当且仅当图中不含奇数环
模板:
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// 参数:u表示当前节点,c表示当前点的颜色
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (color[j] == -1)
{
if (!dfs(j, !c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true;
for (int i = 1; i <= n; i ++ )
if (color[i] == -1)
if (!dfs(i, 0))
{
flag = false;
break;
}
return flag;
}
原题链接:https://www.acwing.com/problem/content/862/
#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010, M = 200010;
int idx,e[M],ne[M],h[N],color[N];
int n,m;
void add(int a,int b)
{
e[idx] = b , ne[idx] = h[a], h[a] = idx ++ ;
}
bool dfs(int u,int c)//u是点,c是颜色
{
color[u] = c;
for(int i = h[u];i!=-1;i=ne[i])
{
int j = e[i];
if(!color[j])
{
if(!dfs(j,3-c)) return false; // 因为颜色从1变成2,从2变成1,所以是3-c
}
else if(color[j] == c) return false;
}
return true;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b), add(b,a);
}
bool flag = true;
for(int i = 1 ; i <= n ; i ++ )
{
if(!color[i])
{
if(!dfs(i,1))
{
flag = false;
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}匈牙利算法
原题链接: https://www.acwing.com/problem/content/863/
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510, M = 100010;
int idx,h[N],e[M],ne[M];
int n1,n2,m;
bool st[N];
int match[N];
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{
for(int i = h[x] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(!st[j])
{
st[j] = true;
if(match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
int main()
{
scanf("%d%d%d",&n1,&n2,&m);
memset(h,-1,sizeof h);
for(int i = 0 ; i < m ; i ++ )
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
}
int res = 0 ;
for(int i = 1 ; i <= n1 ; i ++ )
{
memset(st,false,sizeof st);
if(find(i)) res ++ ;
}
printf("%d",res);
return 0;
}
提高课(搜索)
BFS
Flood Fill
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1010;
typedef pair<int,int> PII;
int n,m;
char g[N][N];
bool st[N][N];
int dx[8] = {-1,-1,-1,0,0,1,1,1}, dy[8] = {-1,0,1,1,-1,0,1,-1};
void bfs(int i,int j){
queue<PII> q;
q.push({i,j});
while(!q.empty()){
auto t = q.front();
q.pop();
st[t.first][t.second] = true;
for(int i = 0; i < 8 ; i ++ ){
int x = t.first + dx[i], y = t.second + dy[i];
if(x >= 0 && x < n && y >= 0 && y <= m && g[x][y] == 'W' && !st[x][y]){
q.push({x,y});
st[x][y] = true;
}
}
}
return ;
}
int main(){
cin >> n >> m;
for(int i = 0 ; i < n ; i ++ ){
cin >> g[i];
}
int res = 0;
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < m ; j ++ ){
if(!st[i][j] && g[i][j] == 'W'){
res ++ ;
bfs(i, j);
}
}
}
cout << res << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 55, M = N * N;
int n,m;
int g[N][N];
PII q[M];
bool st[N][N];
int bfs(int sx,int sy)
{
int dx[4] = {0,-1,0,1}, dy[4] = {-1,0,1,0};
int area = 0;
int hh = 0 , tt = 0;
q[0] = {sx,sy};
st[sx][sy] = true;
while(hh <= tt)
{
PII t = q[hh++];
area ++;
for(int i = 0 ; i < 4 ; i ++ )
{
int a = t.x + dx[i], b = t.y + dy[i];
if(a<0 || a>= m || b < 0 || b >= n ) continue;
if(st[a][b]) continue;
if(g[t.x][t.y] >> i & 1) continue;
q[++tt] = {a,b};
st[a][b] = true;
}
}
return area;
}
int main()
{
cin >> m >> n;
for(int i = 0 ; i < m ; i ++ )
for(int j = 0 ; j < n ; j ++ )
cin >> g[i][j];
int cnt = 0, area = 0;
for(int i = 0 ; i < m ; i ++ )
for(int j = 0 ; j < n ; j ++ )
if(!st[i][j])
{
area = max(area, bfs(i,j));
cnt ++ ;
}
cout << cnt << endl;
cout << area << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 1010, M = N * N;
int n;
int h[N][N];
PII q[M];
bool st[N][N];
void bfs(int sx,int sy,bool& has_higher, bool& has_lower)
{
int hh = 0 , tt = 0;
q[0] = {sx,sy};
st[sx][sy] = true;
while(hh<=tt)
{
PII t = q[hh++];
for(int i = t.x - 1 ; i <= t.x + 1 ; i ++ )
for(int j = t.y - 1 ; j <= t.y + 1 ; j ++ )
{
if(i == t.x && j == t.y) continue;
if(i < 0 || i >= n || j < 0 || j >= n ) continue;
if(h[i][j] != h[t.x][t.y]) //如果高度不同
{
if(h[i][j] > h[t.x][t.y]) has_higher = true;
else has_lower = true;
}else if(!st[i][j])
{
q[++tt] = {i,j};
st[i][j] = true;
}
}
}
}
int main()
{
scanf("%d",&n);
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < n ; j ++ )
scanf("%d",&h[i][j]);
int peak = 0, valley = 0;
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < n ; j ++ )
if(!st[i][j])
{
bool has_higher = false, has_lower = false;
bfs(i,j,has_higher,has_lower);
if(!has_higher) peak++; //没有比它高的说明是山峰
if(!has_lower) valley++;
}
cout << peak << ' ' << valley << endl;
return 0;
}最短路模型
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1010;
typedef pair<int,int> PII;
int n;
int maze[N][N];
int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
PII pre[N][N];
void bfs(int i,int j){
queue<PII> q;
q.push({i,j});
memset(pre, -1, sizeof pre);
pre[i][j] = {0,0};
while(!q.empty()){
auto t = q.front();
q.pop();
for(int i = 0; i < 4 ; i ++ ){
int x = t.first + dx[i], y = t.second + dy[i];
if(x < 0 || x >= n || y < 0 || y >= n ) continue;
if(pre[x][y].first != -1 || maze[x][y] == 1) continue;
q.push({x,y});
pre[x][y] = t;
}
}
}
int main()
{
cin >> n ;
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
cin >> maze[i][j];
}
}
bfs(n - 1, n - 1); //从终点遍历,可使得最后输出的点为正向
PII end(0,0); //起点
while(true){
cout << end.first << ' ' << end.second <<endl;
if(end.first == n - 1 && end.second == n - 1) break;
end = pre[end.first][end.second];
}
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define x first
#define y second
using namespace std;
const int N = 155;
typedef pair<int,int> PII;
int dx[8] = {-2,-2,-1,-1,1,1,2,2}, dy[8] = {-1,1,2,-2,2,-2,1,-1};
char g[N][N];
int n, m;
int d[N][N];
void bfs(int sx,int sy){
memset(d, -1, sizeof d);
queue<PII> q;
q.push({sx, sy});
d[sx][sy] = 0 ;
while(!q.empty()){
auto t = q.front();
q.pop();
for(int i = 0 ; i < 8 ; i ++ ){
int a = t.x + dx[i], b = t.y + dy[i];
if(a < 0 || a >= n || b < 0 || b >= m) continue;
if(d[a][b] != -1 || g[a][b] == '*') continue;
//if(g[a][b] == 'H') return d[t.x][t.y] + 1;
q.push({a,b});
d[a][b] = d[t.x][t.y] + 1;
}
}
}
int main(){
cin >> m >> n;
int kx,ky,hx,hy;
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < m ; j ++ )
{
cin >> g[i][j];
if(g[i][j] == 'K')
{
kx = i, ky = j;
}else if(g[i][j] == 'H'){
hx = i, hy = j;
}
}
bfs(kx, ky);
cout << d[hx][hy] << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
int n,k;
int d[N];
int bfs(){
memset(d, -1, sizeof d);
queue<int> q;
q.push(n);
d[n] = 0;
while(!q.empty()){
auto t = q.front();
q.pop();
if(t == k) return d[k];
if(t + 1 < N && d[t + 1] == -1){
d[t + 1] = d[t] + 1;
q.push(t+1);
}
if(t - 1 >= 0 && d[t - 1] == -1){
d[t - 1] = d[t] + 1;
q.push(t-1);
}
if(t * 2 < N && d[t * 2] == -1){
d[t * 2] = d[t] + 1;
q.push(t*2);
}
}
}
int main(){
cin >> n >> k;
cout << bfs() << endl;
return 0;
}多源bfs
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define x first
#define y second
using namespace std;
const int N = 1010;
typedef pair<int,int> PII;
int n,m;
char A[N][N];
queue<PII> q;
int d[N][N];
int dx[4] = {-1,0,1,0} , dy[4] = {0,1,0,-1};
int main(){
cin >> n >> m;
memset(d, -1, sizeof d);
for(int i = 0 ; i < n ; i++ ){
for(int j = 0 ; j < m ; j ++ ){
cin >> A[i][j];
if(A[i][j] == '1'){
q.push({i,j});
d[i][j] = 0;
}
}
}
while(!q.empty()){
auto t = q.front();
q.pop();
for(int i = 0 ; i < 4 ; i ++ ){
int a = t.x + dx[i], b = t.y + dy[i];
if(a < 0 || a >= n || b < 0 || b >= m) continue;
if(d[a][b] != -1) continue;
q.push({a,b});
d[a][b] = d[t.x][t.y] + 1;
}
}
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < m ; j ++){
cout << d[i][j] << ' ' ;
}
cout << endl;
}
return 0;
}最小步数模型
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
using namespace std;
char a[10],b[10];
map<string,int> dist;//{字符串,变化次数}
map<string,pair<char,string>> pre; //{新字符串,{A/B/C,原字符串}}
string eend;//用end有歧义
string get(string t, int op)
{
string k;
if( op == 0 ) k = {t[7], t[6], t[5], t[4], t[3], t[2], t[1], t[0]};//'A'
if( op == 1 ) k = {t[3], t[0], t[1], t[2], t[5], t[6], t[7], t[4]};//'B'
if( op == 2 ) k = {t[0], t[6], t[1], t[3], t[4], t[2], t[5], t[7]};//'C'
return k;
}
int bfs()
{
string s = "12345678";
queue<string> q;
dist[s] = 0;
q.push(s);
while(!q.empty())
{
auto t = q.front();
q.pop();
if(t == eend) return dist[t];
for(int i = 0 ; i < 3 ; i ++ )
{
string s = get(t,i);
if(!dist.count(s))
{
dist[s] = dist[t] + 1;
pre[s] = {'A' + i, t};
q.push(s);
}
}
}
}
int main()
{
string start = "12345678", res;
for(int i = 1 ; i <= 8 ; i ++ ) cin >> a[i];
for(int i = 1 ; i <= 8 ; i ++ ) eend.push_back(a[i]);
cout << bfs() << endl;
while(eend != start)
{
res += pre[eend].first;
eend = pre[eend].second;
}
reverse(res.begin(), res.end());
cout << res ;
}双向广搜
一般用到最小步数模型里,而不是flood fill和最短路模型里
#include<iostream>
#include<algorithm>
#include<map>
#include<cstring>
#include<queue>
using namespace std;
const int N = 6;
int n;
string A,B; //A是起始串,B是终止串
string a[N], b[N];//a存储A字串,b存储B字串
int extend(queue<string>& q, unordered_map<string,int>& da, unordered_map<string,int>& db, string a[N], string b[N])
{
int d = da[q.front()];
while(q.size() && da[q.front()] == d)
{
auto t = q.front();
q.pop();
for(int i = 0; i < n ; i ++ )//遍历所有规则
for(int j = 0 ; j < t.size() ; j ++ ) //遍历串
if(t.substr(j, a[i].size()) == a[i]) //如果能够转换
{
string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size()); //a串换为b串
if(db.count(r)) return da[t] + db[r] + 1;
if(da.count(r)) continue;
da[r] = da[t] + 1;
q.push(r);
}
}
return 11;
}
int bfs()
{
//BFS的扩展方式是:分别枚举在原字符串中使用替换规则的起点,和所使用的的替换规则。
if(A == B) return 0;
queue<string> qa, qb;
unordered_map<string, int> da,db;//分别存储转换到该串需要几次
qa.push(A), qb.push(B);
da[A] = db[B] = 0;
int step = 0;
while(qa.size() && qb.size())
{
int t;
if(qa.size() < qb.size()) t = extend(qa, da, db, a, b); //从前往后扩展是a->b
else t = extend(qb, db, da, b ,a);//从后往前扩展是b->a
if(t <= 10) return t;
if(++step == 10) return -1;
}
return -1;
}
int main()
{
cin >> A >> B;
while(cin >> a[n] >> b[n]) n++;
int t = bfs();
if(t == -1) puts("NO ANSWER!");
else cout << t << endl;
return 0;
}双端队列广搜
只包含0和1的两种边权重类型的最短路问题
若扩展出来的边权重是0,则插入到队头,若为1,则插入到队尾


#include <cstring>
#include <iostream>
#include <algorithm>
#include <deque>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 510, M = N * N;
int n, m;
char g[N][N];
int dist[N][N];
int bfs()
{
memset(dist, 0x3f, sizeof dist);
dist[0][0] = 0;
deque<PII> q;
q.push_back({0,0});
char cs[] = "\\/\\/" ; //存储的是\/\/,因为\是转义,所以写两个
int dx[4] = {-1,-1,1,1}, dy[4] = {-1,1,1,-1}; //枚举每个点的对角线上的点
int ix[4] = {-1,-1,0,0}, iy[4] = {-1,0,0,-1}; //枚举某个点的邻边
while(q.size())
{
PII t = q.front();
q.pop_front();
for(int i = 0 ; i < 4 ; i ++ )
{
int a = t.x + dx[i], b = t.y + dy[i];
if(a < 0 || a > n || b < 0 || b > m) continue;
int ca = t.x + ix[i], cb = t.y + iy[i];
int d = dist[t.x][t.y] + (g[ca][cb] != cs[i]);
if(d < dist[a][b])
{
dist[a][b] = d;
if(g[ca][cb] != cs[i]) q.push_back({a,b});//需要变化时插尾
else q.push_front({a,b}); //不需要变化时插头
}
}
}
return dist[n][m];
}
int main()
{
int T;
cin >> T;
while(T--)
{
cin >> n >> m;
for(int i = 0 ; i < n ; i ++ ) cin >> g[i];
if(n + m & 1) puts("NO SOLUTION"); //奇数点一定无解
else cout << bfs() << endl;
}
return 0;
}A*


f[state]是state到终点的估计距离,g[state]是state到终点的真实距离
d[state]是起点到state的距离
A*算法必须保证f[state] <= g[state]
一定保证有解才可以搜,否则不如普通bfs
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>
using namespace std;
//估价函数:当前状态中每个数与它的目标位置的曼哈顿距离之和
int f(string state)//求曼哈顿距离
{
int res = 0;
for (int i = 0; i < state.size(); i ++ )
if (state[i] != 'x')
{
int t = state[i] - '1';
res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
}
return res;
}
string bfs(string start)
{
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
char op[4] = {'u', 'r', 'd', 'l'};
string end = "12345678x";
unordered_map<string, int> dist; //存储实际距离
unordered_map<string, pair<string, char>> prev;// {新串,{源串,变换记录}}
priority_queue<pair<int, string>, vector<pair<int, string>>, greater<pair<int, string>>> heap;//小根堆
heap.push({f(start), start});
dist[start] = 0;
while (heap.size())
{
auto t = heap.top();
heap.pop();
string state = t.second;
if (state == end) break;
int step = dist[state];
int x, y;
for (int i = 0; i < state.size(); i ++ )
if (state[i] == 'x')
{
x = i / 3, y = i % 3;//找到x的横纵坐标
break;
}
string source = state;
for (int i = 0; i < 4; i ++ ) //扩展x
{
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 3 && b >= 0 && b < 3)
{
swap(state[x * 3 + y], state[a * 3 + b]);
if (!dist.count(state) || dist[state] > step + 1)
//除了终点之外,当第一次搜到某个点的时候,距离不一定是最短的,其dist[]的值是不断变小的,所以要加后面一个判断
{
dist[state] = step + 1;
prev[state] = {source, op[i]};
heap.push({dist[state] + f(state), state});//实际距离加估算距离放入堆
}
swap(state[x * 3 + y], state[a * 3 + b]);
}
}
}
string res;
while (end != start)
{
res += prev[end].second;
end = prev[end].first;
}
reverse(res.begin(), res.end());
return res;
}
int main()
{
string g, c, seq;//seq存储无x的字符串
while (cin >> c)
{
g += c;
if (c != "x") seq += c;
}
int t = 0;//求逆序对个数
for (int i = 0; i < seq.size(); i ++ )
for (int j = i + 1; j < seq.size(); j ++ )
if (seq[i] > seq[j])
t ++ ;
if (t % 2) puts("unsolvable");//奇数个逆序对无解
else cout << bfs(g) << endl;
return 0;
}
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
typedef pair<int, PII> PIII;
const int N = 1010, M = 200010;
int n,m,S,T,K;
int h[N],rh[N],e[M],w[M],ne[M],idx;
int dist[N],cnt[N];
bool st[N];
void add(int h[],int a,int b,int c)
{
e[idx] = b,w[idx] = c,ne[idx] = h[a], h[a] = idx++;
}
//估计距离:通过反向邻接表djkstra算法求出终点到所有点的最短距离
void djsktra()
{
priority_queue<PII,vector<PII>,greater<PII>> heap;
heap.push({0,T});
memset(dist, 0x3f,sizeof dist);
dist[T] = 0;
while(heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.y;
if(st[ver]) continue;
st[ver] = true;
for(int i = rh[ver]; ~i; i = ne[i])
{
int j = e[i];
if(dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j],j});
}
}
}
}
int astar()
{
priority_queue<PIII,vector<PIII>,greater<PIII>> heap;
heap.push({dist[S],{0,S}});
while(heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.y.y, distance = t.y.x;
cnt[ver] ++ ;
if(cnt[T] == K) return distance;
for(int i = h[ver]; ~i ; i = ne[i])
{
int j = e[i];
if(cnt[j] < K)
heap.push({distance + w[i] + dist[j], {distance + w[i], j}});
}
}
return -1;
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h); //正向邻接表
memset(rh, -1, sizeof rh); //反向邻接表
for(int i = 0 ; i < m ; i ++ )
{
int a,b,c;
cin >> a >> b >> c;
add(h, a, b, c);
add(rh, b, a, c);
}
cin >> S >> T >> K;
if(S == T) K ++ ;
djsktra();
cout << astar() << endl;
return 0;
}DFS
连通性模型
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int Q;
int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
bool st[N][N];
char g[N][N];
int n;
int ha, la, hb, lb;
bool dfs(int ha,int la){
if(g[ha][la] == '#') return false;
if(ha == hb && la == lb){
return true;
}
st[ha][la] = true;
for(int i = 0; i < 4 ; i ++ ){
int x = ha + dx[i] , y = la + dy[i];
if(x < 0 || x >= n || y < 0 || y >= n ) continue;
if(st[x][y]) continue;
if(dfs(x,y)) return true;
}
return false;
}
int main(){
cin >> Q;
while(Q--){
memset (st,false,sizeof (st));
cin >> n;
for(int i = 0; i < n ; i ++ ){
for(int j = 0; j < n ; j ++ ){
cin >> g[i][j];
}
}
cin >> ha >> la >> hb >> lb;
if(dfs(ha,la)) cout <<"YES" << endl;
else cout << "NO" << endl;
}
return 0;
}#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 25;
int w,h;
char g[N][N];
bool st[N][N];
int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
int dfs(int x,int y){
int cnt = 1;
st[x][y] = true;
for(int i = 0 ; i < 4 ; i ++ ){
int a = x + dx[i], b = y + dy[i];
if(a < 0 || a >= h || b < 0 || b >= w) continue;
if(st[a][b] || g[a][b] == '#') continue;
cnt += dfs(a,b);
}
return cnt;
}
int main(){
while(cin >> w >> h , w || h){
int x,y;
for(int i = 0 ; i < h ; i ++ )
for(int j = 0 ; j < w ; j ++ )
{
cin >> g[i][j];
if(g[i][j] == '@')
{
x = i, y = j;
}
}
memset(st, 0, sizeof st);
cout << dfs(x,y) << endl;
}
return 0;
}搜索顺序
当为内部搜索,比如一个棋盘它本身的状态进行改变时,需要用到中间状态,则需要回溯;当为外部搜索,比如一个棋盘某个点到另一个点的连通性,不用考虑中间状态,则不需要回溯
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 10;
int T;
int n,m;
int x,y;
int g[N][N];
bool st[N][N];
int dx[8] = {-2,-1,1,2,2,1,-1,-2}, dy[8] = {1,2,2,1,-1,-2,-2,-1};
int res;
void dfs(int x,int y,int cnt){
if(cnt == n * m){
res ++ ;
return ;
}
st[x][y] = true;
for(int i = 0 ; i < 8 ; i ++ ){
int a = x + dx[i], b = y + dy[i];
if(a < 0 || a >= n || b < 0 || b >= m ) continue;
if(st[a][b]) continue;
dfs(a,b, cnt + 1);
}
st[x][y] = false;
}
int main(){
cin >> T;
while(T --){
cin >> n >> m >> x >> y;
res = 0;
dfs(x, y, 1);
cout << res << endl;
}
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 25;
int n;
string word[N];
int g[N][N];//g[i][j] 表示word[i]的后缀和word[j]的前缀的最小相同长度
int used[N];
int res;
void dfs(string dragon,int last){//last表示上个字符串下标
res = max((int)dragon.size(), res);
used[last] ++ ;
for(int i = 0 ; i < n ; i ++ ){
if(g[last][i] && used[i] < 2){
dfs(dragon + word[i].substr(g[last][i]), i);
//substr()函数若只有一个参数,说明是从某个位置到末尾
//该语句是将龙头加上新的拼接字符串作为新的龙头,进而不断递归
}
}
used[last] -- ;
}
int main(){
cin >> n;
for(int i = 0 ; i < n ; i ++ ){
cin >> word[i];
}
char start;
cin >> start;
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
string a = word[i], b = word[j];
for(int k = 1 ; k < min(a.size(), b.size()); k ++ ){
if(a.substr(a.size() - k, k) == b.substr(0,k)){
g[i][j] = k;
break;
}
}
}
}
for(int i = 0 ; i < n ; i ++ ){
if(word[i][0] == start)
dfs(word[i], i);
}
cout << res << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 10;
int n;
int p[N];
int group[N][N];//group[i]表示第i组中下标对应的p数组中的数互质
bool st[N];
int res = N; //最坏情况分为N组
int gcd(int a,int b){ //判断是否互质(求最大公因数)
return b ?gcd(b, a % b): a;
}
bool check(int group[],int gc,int i){
for(int j = 0 ; j < gc ; j ++ ){
if(gcd(p[group[j]], p[i]) > 1)
return false;
}
return true;
}
//g表示当前做到了哪一组,gc表示当前枚举到组内的第几个元素,tc表示当前一共处理多少个数,start表示组内从哪个数开始枚举
void dfs(int g,int gc,int tc,int start){
if(g >= res) return ;
if(tc == n) res = g; //所有数均处理完
bool flag = true;
for(int i = start ; i < n ; i ++ ) {
if(!st[i] && check(group[g], gc, i))
{
st[i] = true;
group[g][gc] = i;
dfs(g, gc + 1, tc + 1, i + 1);
st[i] = false;
flag = false;
}
}
if(flag) dfs(g + 1,0, tc, 0); //如果没找到互质的,则开启下一组
return ;
}
int main()
{
cin >> n;
for(int i = 0 ; i < n ; i ++ ) cin >> p[i];
dfs(1,0,0,0);
cout << res << endl;
return 0;
}剪枝与优化

1 -> 猫按照重量由大到小排序,先放重猫(优先考虑决策少的方案)
3 -> 当前某个猫放到车上超出车承重,直接删去
4 -> 某个方案大于res,直接剪枝
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 20;
int cat[N], cab[N];
int n, w;
int res = N;
bool cmp(int a,int b){
return a > b;
}
//第u条猫,第k辆车
void dfs(int u, int k){
//最优性剪枝
if(k >= res) return ;
if(u == n){
res = k;
return ;
}
for(int i = 0 ; i < k ; i ++ ){
if(cab[i] + cat[u] <= w){
cab[i] += cat[u];
dfs(u + 1, k);
cab[i] -= cat[u];
}
}
//新开一辆车
cab[k] = cat[u];
dfs(u + 1, k + 1);
cab[k] = 0;
}
int main(){
cin >> n >> w;
for(int i = 0 ; i < n ; i++ ) cin >> cat[i];
sort(cat, cat + n, cmp);
dfs(0,0);
cout << res << endl;
}#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 9, M = 1 << N;
//用一个二进制数表示当前行,或列或方格的状态,如100110010,则表示可填的是1,4,5,8
int ones[M], map[M];//ones保存每个状态有多少个1,map[i]保存lg(i)为多少
int row[N], col[N], cell[3][3];
char str[100];
void init()
{
for (int i = 0; i < N; i ++ )
row[i] = col[i] = (1 << N) - 1;
for (int i = 0; i < 3; i ++ )
for (int j = 0; j < 3; j ++ )
cell[i][j] = (1 << N) - 1;
}
void draw(int x, int y, int t, bool is_set)//若is_set是true,则是在(x,y)添加t,若is_set是false,则是删去(x,y)这个数
{
if (is_set) str[x * N + y] = '1' + t;
else str[x * N + y] = '.';
int v = 1 << t;
if (!is_set) v = -v;
row[x] -= v;
col[y] -= v;
cell[x / 3][y / 3] -= v;
}
int lowbit(int x)//返回二进制的最后一位1
{
return x & -x;
}
int get(int x, int y)//找到所有可填的二进制状态
{
return row[x] & col[y] & cell[x / 3][y / 3];
}
bool dfs(int cnt)
{
if (!cnt) return true;
int minv = 10;
int x, y;
for (int i = 0; i < N; i ++ )
for (int j = 0; j < N; j ++ )
if (str[i * N + j] == '.')
{
int state = get(i, j);
if (ones[state] < minv)
{
minv = ones[state];
x = i, y = j;
}
}
int state = get(x, y);
for (int i = state; i; i -= lowbit(i))
{
int t = map[lowbit(i)];
draw(x, y, t, true);
if (dfs(cnt - 1)) return true;
draw(x, y, t, false);
}
return false;
}
int main()
{
for (int i = 0; i < N; i ++ ) map[1 << i] = i;
for (int i = 0; i < 1 << N; i ++ )
for (int j = 0; j < N; j ++ )
ones[i] += i >> j & 1;
while (cin >> str, str[0] != 'e')
{
init();
int cnt = 0;
for (int i = 0, k = 0; i < N; i ++ )
for (int j = 0; j < N; j ++, k ++ )
if (str[k] != '.')
{
int t = str[k] - '1';
draw(i, j, t, true);
}
else cnt ++ ;
dfs(cnt);
puts(str);
}
return 0;
}
先从小到大枚举木棒的长度,对于每个长度,从前往后依此拼接木棍,从而找到合法方案
1 -> 先枚举长度更长的木棍
2 -> 排除等效冗余:(1)按照组合数的方式枚举(2)如果当前木棍加到当前棒中失败了,则直接略过后面所有长度相等的木棍
(3)如果木棒的第一根木棍失败了,则该方案一定失败(4)如果木棒的最后一根木棍失败了,则该方案一定失败
3 -> 只枚举木棍长度和sum的约数
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 70;
int n;
int w[N];
int sum,length;
bool st[N];
bool dfs(int u,int cur,int start) //u枚举木棒的个数,cur表示当前已经接上木棍的长度,start表示枚举的木棍下标
{
if(u * length == sum) return true;
if(cur == length) return dfs(u + 1, 0, 0);
//剪枝3-1,i从start开始枚举
for(int i = start; i < n ; i ++ )
{
if(st[i] || cur + w[i] > length) continue; //可行性剪枝
st[i] = true;
if(dfs(u,cur + w[i], i + 1)) return true;
st[i] = false;
//剪枝3-3和3-4
if(!cur || cur + w[i] == length) return false;
//剪枝3-2
int j = i;
while(j < n && w[j] == w[i]) j ++ ;
i = j - 1;
}
return false;
}
int main()
{
while(cin >> n, n)
{
memset(st,0,sizeof st);
sum = 0;
for(int i = 0; i < n ; i ++ )
{
cin >> w[i];
sum += w[i];
}
//剪枝2,优化搜索顺序
sort(w,w+n);
reverse(w,w+n);
length = 1;
while(true)
{
//剪枝1
if(sum % length == 0 && dfs(0,0,0))
{
cout << length << endl;
break;
}
length ++ ;
}
}
return 0;
}
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 25, INF = 1e9;
int n,m;
int minv[N],mins[N];//前若干层的体积最小值和面积最小值
int R[N], H[N];//每一层的半径和高度
int res = INF;
void dfs(int u,int v,int s) //u枚举的层数,v当前枚举体积,s当前枚举表面积
{
if(v + minv[u] > n) return;
if(s + mins[u] >= res) return;
if(s + 2 * (n - v) / R[u + 1] >= res) return ;
if(!u)
{
if(v == n) res = s;
return ;
}
for(int r = min(R[u+1] - 1,(int)sqrt(n-v)); r >= u; r --)
for(int h = min(H[u+1] - 1,(n-v) /r /r ); h >= u;h -- )
{
int t = 0;
if(u == m) t = r * r;
R[u] = r,H[u] = h;
dfs(u - 1, v + r * r * h, s + 2 * r * h + t);
}
}
int main()
{
cin >> n >> m;
for(int i = 1 ; i <= m ; i ++ )
{
minv[i] = minv[i-1] + i * i * i;
mins[i] = mins[i-1] + 2 * i * i;
}
R[m + 1] = H[m + 1] = INF;
dfs(m, 0, 0);
if(res == INF) res = 0;
cout << res << endl;
return 0;
}迭代加深
适合于某些分支特别深,但是答案在比较浅的分支的问题
剪枝1:优先枚举较大的数
剪枝2:排除等效冗余,如果某两对数和相等,只需要枚举其中一对
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int path[N] ;
int n;
//u当前迭代的点,k当前迭代的层数
bool dfs(int u,int k){
if(u == k) return path[u - 1] == n;
bool st[N] = {0};
for(int i = u - 1; i >= 0 ; i -- ){
for(int j = i ; j >= 0 ; j -- ){
int s = path[i] + path[j];
if(s > n || s <= path[u - 1] || st[s]) continue;
st[s] = true;
path[u] = s;
if(dfs(u + 1, k)) return true;
}
}
return false;
}
int main(){
path[0] = 1;
while(cin >> n , n){
int k = 1;
while(!dfs(1, k)) k ++ ;
for(int i = 0 ; i < k ; i ++ ){
cout << path[i] << ' ';
}
cout << endl;
}
return 0;
}双向DFS

其中k是指2^k与 2^(N-k)*k相接近最合适的数,这里取了n/2

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1 << 24;
int n, m, k;
int g[50], weights[N];
int cnt = 0;
int ans;
void dfs(int u, int s)
{
if (u == k)
{
weights[cnt ++ ] = s;
return;
}
if ((LL)s + g[u] <= m) dfs(u + 1, s + g[u]);
dfs(u + 1, s);
}
void dfs2(int u, int s)
{
if (u == n)
{
int l = 0, r = cnt - 1;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (weights[mid] + (LL)s <= m) l = mid;
else r = mid - 1;
}
if (weights[l] + (LL)s <= m) ans = max(ans, weights[l] + s);
return;
}
if ((LL)s + g[u] <= m) dfs2(u + 1, s + g[u]);
dfs2(u + 1, s);
}
int main()
{
cin >> m >> n;
for (int i = 0; i < n; i ++ ) cin >> g[i];
sort(g, g + n);
reverse(g, g + n);
k = n / 2; // 防止 n = 1时,出现死循环
dfs(0, 0);
sort(weights, weights + cnt);
int t = 1;
for (int i = 1; i < cnt; i ++ )
if (weights[i] != weights[i - 1])
weights[t ++ ] = weights[i];
cnt = t;
dfs2(k, 0);
cout << ans << endl;
return 0;
}
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 46;
int n,m,k;
int w[N];
int weights[1 << 25], cnt = 1;
int ans; //全局最小值
//u是当前枚举到的数,s是当前的和
void dfs1(int u,int s){
if(u == k){
weights[cnt ++ ] = s;
return ;
}
dfs1(u + 1, s) ; //不选当前的物品
if((LL)s + w[u] <= m) dfs1(u + 1, s + w[u]); //选当前物品
}
void dfs2(int u,int s){
if(u >= n){ //二分求出w - s的最大值
int l = 0 , r = cnt - 1;
while(l < r){
int mid = l + r + 1 >> 1;
if(weights[mid] <= m - s) l = mid;
else r = mid - 1;
}
ans = max(ans, weights[l] + s);
return ;
}
dfs2(u + 1, s);
if((LL) s + w[u] <= m) dfs2(u + 1, s + w[u]);
}
int main()
{
cin >> m >> n;
for(int i = 0 ; i < n ; i ++ ) cin >> w[i];
sort(w, w + n);
reverse(w, w + n);
k = n >> 1;
dfs1(0, 0);
sort(weights, weights + cnt);
cnt = unique(weights, weights + cnt) - weights; //判重
dfs2(k, 0);
cout << ans << endl;
return 0;
}IDA*
估价函数:total/3上取整(total存的是错误后继的数量,后面一个数比前面一个大1就是一个正确的后继
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 15;
int n;
int q[N]; // 存储该序列
int w[5][N]; // 存储现场,方便恢复现场
int f() // 估价函数
{
int cnt = 0;
for(int i = 0 ; i + 1 < n ; i ++ )
if(q[i + 1] != q[i] + 1)
cnt ++ ;
return (cnt + 2) / 3;
}
bool check() //检查是否有错误后继
{
for(int i = 0; i + 1 < n ; i ++ )
if(q[i + 1] != q[i] + 1)
return false;
return true;
}
bool dfs(int depth, int max_depth)//当前迭代深度,最大迭代深度
{
if (depth + f() > max_depth) return false;
if (check()) return true;
for (int len = 1; len <= n; len ++ )
for (int l = 0; l + len - 1 < n; l ++ )
{
int r = l + len - 1;
for (int k = r + 1; k < n; k ++ )
{
memcpy(w[depth], q, sizeof q);
int x, y;
for (x = r + 1, y = l; x <= k; x ++, y ++ ) q[y] = w[depth][x];
for (x = l; x <= r; x ++, y ++ ) q[y] = w[depth][x];
if (dfs(depth + 1, max_depth)) return true;
memcpy(q, w[depth], sizeof q);
}
}
return false;
}
int main()
{
int T;
cin >> T;
while(T --)
{
cin >> n;
for(int i = 0 ; i < n ; i ++ ) cin >> q[i];
int depth = 0;
while(depth < 5 && !dfs(0,depth)) depth ++ ;
if(depth >= 5) puts("5 or more");
else cout << depth << endl;
}
return 0;
}估价函数:设中间八个数重复次数最多的数是s次,则其估价函数为8-s
/*
0 1
2 3
4 5 6 7 8 9 10
11 12
13 14 15 16 17 18 19
20 21
22 23
*/
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 24;
int op[8][7] = {
{0, 2, 6, 11, 15, 20, 22},
{1, 3, 8, 12, 17, 21, 23},
{10, 9, 8, 7, 6, 5, 4},
{19, 18, 17, 16, 15, 14, 13},
{23, 21, 17, 12, 8, 3, 1},
{22, 20, 15, 11, 6, 2, 0},
{13, 14, 15, 16, 17, 18, 19},
{4, 5, 6, 7, 8, 9, 10}
};
int oppsite[8] = {5, 4, 7, 6, 1, 0, 3, 2};
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};
int q[N];
int path[100];
int f() //估价函数
{
static int sum[4];
memset(sum, 0, sizeof sum);
for (int i = 0; i < 8; i ++ ) sum[q[center[i]]] ++ ;
int maxv = 0;
for (int i = 1; i <= 3; i ++ ) maxv = max(maxv, sum[i]);
return 8 - maxv;
}
void operate(int x) //模拟八个操作
{
int t = q[op[x][0]];
for (int i = 0; i < 6; i ++ ) q[op[x][i]] = q[op[x][i + 1]];
q[op[x][6]] = t;
}
bool dfs(int depth, int max_depth, int last) //当前深度,最大深度,上个操作
{
if (depth + f() > max_depth) return false;
if (f() == 0) return true;
for (int i = 0; i < 8; i ++ )
if (last != oppsite[i])
{
operate(i);
path[depth] = i;
if (dfs(depth + 1, max_depth, i)) return true;
operate(oppsite[i]);
}
return false;
}
int main()
{
while (cin >> q[0], q[0])
{
for (int i = 1; i < 24; i ++ ) cin >> q[i];
int depth = 0;
while (!dfs(0, depth, -1)) depth ++ ;
if (!depth) printf("No moves needed");
else
{
for (int i = 0; i < depth; i ++ ) printf("%c", 'A' + path[i]);
}
printf("\n%d\n", q[6]);
}
return 0;
}
提高课(图论)
单源最短路的建图方式
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 2510, M = 2*6210;
int n,m,ts,te;
int idx,e[M],ne[M],w[M],h[N];
int d[N];
bool st[N];
void add(int a,int b,int c){
e[idx] = b,w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
memset(d, 0x3f, sizeof d);
d[ts] = 0;
priority_queue<PII, vector<PII>,greater<PII>> heap;
heap.push({0,ts});
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if(d[j] > dis + w[i]){
d[j] = dis + w[i];
heap.push({d[j], j});
}
}
}
return d[te];
}
int main()
{
memset(h, -1,sizeof h);
cin >> n >> m >> ts >> te;
for(int i = 0 ; i < m ; i ++ )
{
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
add(b,a,c);
}
int t = dijkstra();
cout << t << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 110, M = 210 * 2;
int idx,e[M],ne[M],w[M],h[N];
int n,m;
bool st[N];
int d[N];
void add(int a,int b,int c){
e[idx] = b, w[idx] = c,ne[idx] = h[a], h[a] = idx++;
}
int dijkstra(){
memset(d, 0x3f, sizeof d);
d[1] = 0;
priority_queue<PII,vector<PII>,greater<PII>> heap;
heap.push({0, 1});
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1 ; i = ne[i]){
int j = e[i];
if(d[j] > dis + w[i]){
d[j] = dis + w[i];
heap.push({d[j], j});
}
}
}
int res;
for(int i = 1 ; i <= n ; i ++ ){
if(d[i] > 0x3f3f3f3f /2 ) return -1;
res = max(res, d[i]);
}
return res;
}
int main()
{
memset(h, -1,sizeof h);
cin >> n >> m ;
for(int i = 0 ; i <m ; i ++ ){
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
int t = dijkstra();
cout << t << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 810, M = 1460 * 2;
int n,p,c;
int idx,e[M],ne[M],w[M],h[N];
bool st[N];
int d[N];
int num[N];
void add(int a,int b,int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int dijkstra(int s){
memset(st, false, sizeof st);
memset(d, 0x3f, sizeof d);
d[s] = 0;
priority_queue<PII,vector<PII>,greater<PII>> heap;
heap.push({0,s});
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if(d[j] > dis + w[i]) {
d[j] = dis + w[i];
heap.push({d[j], j});
}
}
}
int ans = 0;
for(int i = 0 ; i < n ; i ++ ){
if(d[num[i]] > 0x3f3f3f3f /2 ) return 0x3f3f3f3f;
ans += d[num[i]];
}
return ans;
}
int main(){
memset(h, -1,sizeof h);
cin >> n >> p >> c;
for(int i = 0 ; i < n ; i ++ ) cin >> num[i];
for(int i = 0 ; i < c ; i ++ ){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
add(y,x,z);
}
int res = 0x3f3f3f3f;
for(int i = 1; i <= p ; i ++ ) res = min(res,dijkstra(i));
cout << res << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<double,int> PII;
const int N = 2010, M = 1e5 * 2 + 10;
int idx,e[M], ne[M], w[M], h[N];
int n, m, A, B;
bool st[N];
double d[N];
void add(int a,int b,int c){
e[idx] = b ,w[idx] = c, ne[idx] = h[a], h[a] = idx++ ;
}
double dijkstra(){
for(int i = 1 ; i <= n ; i++ ) d[i] = 0x3f3f3f3f;
d[B] = 100;
priority_queue<PII,vector<PII>,greater<PII>> heap;
heap.push({100,B});
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second;
double dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if(d[j] > dis * 100 /(100 - w[i])){
d[j] = dis * 100 /(100 - w[i]);
heap.push({d[j], j});
}
}
}
return d[A];
}
int main(){
cin >> n >> m;
memset(h ,-1, sizeof h);
for(int i = 0 ; i < m ; i ++ ){
int a,b,c;
cin >> a >> b >> c;
add(b, a, c);
add(a, b, c);
}
cin >> A >> B;
double t = dijkstra();
printf("%.8lf\n", t);
return 0;
}#include<iostream>
#include<cstring>
#include<algorithm>
#include<sstream>
#include<queue>
using namespace std;
const int N = 510, M = 110;
int n,m;
bool g[N][N];
int d[N];
bool st[N];
int stop[N];
void bfs(){
memset(d, 0x3f, sizeof d);
queue<int> q;
q.push(1);
d[1] = 0 ;
while(!q.empty()){
auto t = q.front();
q.pop();
for(int i = 1 ; i <= n ; i ++){
if(g[t][i] && d[i] > d[t] + 1){
d[i] = d[t] + 1;
q.push(i);
}
}
}
}
int main()
{
cin >> m >> n ;
string line;
getline(cin,line); //读入换行符
for(int i = 0 ; i < m ; i ++ ){
getline(cin ,line);
stringstream ssin(line);
int cnt = 0, p ;
while(ssin >> p ) stop[cnt ++ ] = p;
for(int j = 0 ; j < cnt ; j ++ ){
for(int k = j + 1 ; k < cnt ; k ++ ){
g[stop[j]][stop[k]] = true;
}
}
}
bfs();
if (d[n] == 0x3f3f3f3f) puts("NO");
else cout << max(d[n] - 1,0) << endl;
return 0;
}
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int m,n;
int g[N][N];
int d[N];
int level[N];
bool st[N];
int dijkstra(int lmin, int lmax){
memset(d, 0x3f, sizeof d);
memset(st, false,sizeof st);
d[0] = 0;
for(int i = 0; i < n ; i ++ ){
int t = -1;
for(int j = 0 ; j <= n ; j ++ ){
if(!st[j] && (t == -1 || d[t] > d[j]))
t = j;
}
for(int j = 1 ; j <= n ; j ++ ){
if(level[j] >= lmin && level[j] <= lmax){
d[j] = min(d[j], d[t] + g[t][j]);
}
}
st[t] = true;
}
return d[1];
}
int main(){
memset(g, 0x3f, sizeof g);
for(int i = 1 ; i <= n ;i ++ ){
g[i][i] = 0;
}
cin >> m >> n;
for(int i = 1 ; i <= n ; i ++ ){
int p, l, x ;
cin >> p >> l >> x;
g[0][i] = p;
level[i] = l;
while(x -- ){
int t, v;
cin >> t >> v;
g[t][i] = v;
}
}
int res = INF;
for(int i = level[1] - m ; i <= level[1] ; i ++ ) res = min(res, dijkstra(i, i + m));
cout << res << endl;
return 0;
}单源最短路的综合应用
单源最短路+dfs暴搜
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 50010, M = 1e5 * 2 + 10, INF = 0x3f3f3f3f;
int idx, e[M], ne[M], w[M], h[N];
int n,m;
bool st[N];
int d[6][N];
int source[6];
void add(int a,int b,int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra(int start, int dist[]){
memset(st, false, sizeof st);
memset(dist, 0x3f, N * 4);
priority_queue<PII,vector<PII>, greater<PII>> heap;
heap.push({0,start});
dist[start] = 0;
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver] ; i != -1; i = ne[i]){
int j = e[i];
if(dist[j] > dis + w[i]){
dist[j] = dis + w[i];
heap.push({dist[j], j});
}
}
}
}
//u:枚举到第几个亲戚,start:从哪个亲戚出发,dis:当前的距离
int dfs(int u,int start,int dis){
if(u == 6) return dis;
int res = INF;
for(int i = 1; i <= 5 ; i++){
if(!st[i]){
int next = source[i];
st[i] = true;
res = min(res, dfs(u + 1, i, dis + d[start][next]));
st[i] = false;
}
}
return res;
}
int main(){
cin >> n >> m ;
memset(h ,-1,sizeof h);
source[0] = 1;
for(int i = 1 ; i <= 5 ; i++ ) cin >> source[i];
for(int i = 0 ; i < m ; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
for(int i = 0 ; i < 6 ; i ++) dijkstra(source[i], d[i]);
memset(st, false ,sizeof st);
int res = dfs(1, 0, 0);
cout << res << endl;
return 0;
}通信线路
双端队列广搜+二分


#include<iostream>
#include<algorithm>
#include<cstring>
#include<deque>
using namespace std;
const int N = 1010, M = 20010;
int n,m,k;
int idx, e[M], ne[M], w[M], h[N];
int d[N];
bool st[N];
deque<int> q;
void add(int a,int b,int c){
e[idx] = b, w[idx]= c, ne[idx]= h[a], h[a] = idx ++;
}
bool check(int bound)
{
//求最小的这样一个x,使得大于等于x的边的数量<=k
//双端队列广搜求大于等于x的边的数量
memset(st, 0, sizeof st);
memset(d, 0x3f, sizeof d);
d[1] = 0;
q.push_back(1);
while(q.size()){
auto t = q.front();
q.pop_front();
if(st[t]) continue;
st[t] = true;
for(int i = h[t]; i != -1; i = ne[i]) {
int j = e[i], x = w[i] > bound;
if(d[j] > d[t] + x){
d[j] = d[t] + x;
if(x) q.push_back(j);
else q.push_front(j);
}
}
}
return d[n] <= k;
}
int main(){
cin >> n >> m >> k;
memset(h, -1, sizeof h);
for(int i = 0 ;i < m ;i ++ ){
int a,b,c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
int l = 0, r = 1e6 +1 ;
while(l < r){
int mid = l + r >> 1;
if(check(mid)) r = mid;
else l = mid + 1;
}
if (r == 1e6 + 1) cout << -1 << endl;
else cout << r << endl;
}dfs + 拓扑 + 最短路



#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
typedef pair<int,int> PII;
const int N = 25010, M = 150010, INF = 0x3f3f3f3f;
int n, mr, mp, S, bnt;
int idx, e[M], ne[M], w[M], h[N];
bool st[N];
int d[N];
int id[N];
int din[N];
vector<int> block[N];
queue<int> q;
void add(int a,int b,int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u,int bid){
block[bid].push_back(u);
id[u] = bid;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(!id[j]){
dfs(j, bid);
}
}
}
void dijkstra(int bid){
priority_queue<PII,vector<PII>,greater<PII>> heap;
for(auto it : block[bid]){
heap.push({d[it], it});
}
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i!= -1; i = ne[i]){
int j = e[i];
if(d[j] > dis + w[i]){
d[j] = dis + w[i];
if(id[j] == id[ver]) heap.push({d[j], j});
}
if(id[ver] != id[j] && --din[id[j]] == 0) q.push(id[j]);
}
}
}
void topsort(){
memset(d, 0x3f, sizeof d);
d[S] = 0 ;
for(int i = 1 ; i <= bnt ; i ++){
if(!din[i]){
q.push(i);
}
}
while(q.size()){
auto t = q.front();
q.pop();
dijkstra(t);
}
}
int main()
{
cin >> n >> mr >> mp >> S;
memset(h, -1, sizeof h);
for(int i = 0 ; i < mr ; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
for(int i = 1 ; i <= n ; i ++) {
if(!id[i]){
dfs(i, ++ bnt);
}
}
for(int i = 0 ; i < mp ; i ++) {
int a,b,c;
cin >> a>> b >> c;
add(a, b, c);
din[id[b]] ++ ;
}
topsort();
for(int i = 1 ; i <= n ; i ++ ){
if(d[i] > INF / 2) cout << "NO PATH" << endl;
else cout << d[i] << endl;
}
return 0;
}最优贸易(未做)
dp + 最短路
先求出:
- 从 1走到 i 的过程中,买入水晶球的最低价格 dmin[i];
- 从 i 走到 n 的过程中,卖出水晶球的最高价格 dmax[i];
然后枚举每个城市作为买卖的中间城市,求出 dmax[i] - dmin[i] 的最大值即可。
求 dmin[i] 和 dmax[i] 时,由于不是拓扑图,状态的更新可能存在环,因此不能使用动态规划,只能使用求最短路的方式。
不能用dijsktra算法的原因:
最一般的最短路维护的是路径上的sum性质,本题维护的是max和min性质,sum性质具有累加性(就是要从前面的值基础上累加,后续出现只会越来越大,所以第一次出现的就是最短),而max 和min对于新出现的数,单独比较即可,所以不能用dijkstra(dijkstra就是利用的sum的累加性)
总的来说就是max和min,后面出现的数不一定比前面的数都差(而dijkstra的sum性质能保证后面出现的数都比前面的数都差)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010, M = 2000010;
int n, m;
int price[N];
int h[N], rh[N], e[M], ne[M], idx;
int dmin[N], dmax[N];
bool st[N];
void add(int *h, int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa(int *d, int start, int *h, bool flag)
{
queue<int> q;
memset(st, 0, sizeof st);
if (flag) memset(d, 0x3f, sizeof dmin);
q.push(start);
st[start] = true;
d[start] = price[start];
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (flag && d[j] > min(d[t], price[j]) || !flag && d[j] < max(d[t], price[j]))
{
if (flag) d[j] = min(d[t], price[j]);
else d[j] = max(d[t], price[j]);
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
memset(rh, -1, sizeof rh);
for (int i = 1; i <= n; i ++ ) scanf("%d", &price[i]);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(h, a, b), add(rh, b, a);
if (c == 2) add(h, b, a), add(rh, a, b);
}
spfa(dmin, 1, h, true);
spfa(dmax, n, rh, false);
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, dmax[i] - dmin[i]);
printf("%d\n", res);
return 0;
}单源最短路的扩展方式
虚拟源点

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 1010, M = 30010, INF = 0x3f3f3f3f;
int n,m,s;
int idx, e[M], ne[M], w[M], h[N];
bool st[N];
int d[N];
int cnt;
void add(int a,int b,int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra(){
memset(d, 0x3f, sizeof d);
memset(st, false, sizeof st);
priority_queue<PII,vector<PII>,greater<PII>> heap;
d[0] = 0;
heap.push({0, 0});
while(heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, dis = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if(d[j] > dis + w[i]){
d[j] = dis + w[i];
heap.push({d[j], j});
}
}
}
if(d[s] > INF / 2) return -1;
return d[s];
}
int main()
{
while(cin >> n >> m >> s){
memset(h, -1, sizeof h);
idx = 0;
for(int i = 0 ; i < m ; i ++ ){
int a,b,c;
cin >> a >> b >> c;
add(a, b, c);
}
cin >> cnt ;
for(int i = 0; i < cnt ; i ++ ){
int p;
cin >> p;
add(0, p, 0);
}
int t = dijkstra();
cout << t << endl;
}
return 0;
}拯救大兵瑞恩(未做)

#include <cstring>
#include <iostream>
#include <algorithm>
#include <deque>
#include <set>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 11, M = 360, P = 1 << 10;
int n, m, k, p;
int h[N * N], e[M], w[M], ne[M], idx;
int g[N][N], key[N * N];
int dist[N * N][P];
bool st[N * N][P];
set<PII> edges;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void build()
{
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
for (int u = 0; u < 4; u ++ )
{
int x = i + dx[u], y = j + dy[u];
if (!x || x > n || !y || y > m) continue;
int a = g[i][j], b = g[x][y];
if (!edges.count({a, b})) add(a, b, 0);
}
}
int bfs()
{
memset(dist, 0x3f, sizeof dist);
dist[1][0] = 0;
deque<PII> q;
q.push_back({1, 0});
while (q.size())
{
PII t = q.front();
q.pop_front();
if (st[t.x][t.y]) continue;
st[t.x][t.y] = true;
if (t.x == n * m) return dist[t.x][t.y];
if (key[t.x])
{
int state = t.y | key[t.x];
if (dist[t.x][state] > dist[t.x][t.y])
{
dist[t.x][state] = dist[t.x][t.y];
q.push_front({t.x, state});
}
}
for (int i = h[t.x]; ~i; i = ne[i])
{
int j = e[i];
if (w[i] && !(t.y >> w[i] - 1 & 1)) continue; // 有门并且没有钥匙
if (dist[j][t.y] > dist[t.x][t.y] + 1)
{
dist[j][t.y] = dist[t.x][t.y] + 1;
q.push_back({j, t.y});
}
}
}
return -1;
}
int main()
{
cin >> n >> m >> p >> k;
for (int i = 1, t = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
g[i][j] = t ++ ;
memset(h, -1, sizeof h);
while (k -- )
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
int a = g[x1][y1], b = g[x2][y2];
edges.insert({a, b}), edges.insert({b, a});
if (c) add(a, b, c), add(b, a, c);
}
build();
int s;
cin >> s;
while (s -- )
{
int x, y, c;
cin >> x >> y >> c;
key[g[x][y]] |= 1 << c - 1;
}
cout << bfs() << endl;
return 0;
}
最短路的条数

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, M = 4e5 + 10, MOD = 100003;
int n,m;
int idx, e[M], ne[M], h[N];
int d[N];
int cnt[N];
void add(int a,int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void bfs()
{
memset(d, 0x3f, sizeof d);
queue<int> q;
q.push(1);
d[1] = 0;
cnt[1] = 1;
while(q.size()){
auto t = q.front();
q.pop();
for(int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if(d[j] > d[t] + 1){
d[j] = d[t] + 1;
cnt[j] = cnt[t];
q.push(j);
}
else if(d[j] == d[t] + 1){
cnt[j] = (cnt[t] + cnt[j]) % MOD;
}
}
}
}
int main()
{
memset(h , -1, sizeof h);
cin >> n >> m ;
for(int i = 0; i < m ; i ++ ){
int a,b;
cin >> a >> b;
add(a, b), add(b, a);
}
bfs();
for(int i = 1; i <= n ; i ++ ) cout << cnt[i] << endl;
return 0;
}最短路径的条数
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1010, M = 10010;
int n,m,S,F;
int idx, e[M], ne[M], h[N], w[M];
int d[N][2];
bool st[N][2];
int cnt[N][2];
struct Ver {
int ver, type, dist; //0:最短路,1:次短路
//小根堆重载大于号
bool operator> (const Ver &W) const{
return dist > W.dist;
}
};
void add(int a,int b,int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra(){
memset(st, 0, sizeof st);
memset(d, 0x3f, sizeof d);
memset(cnt, 0, sizeof cnt);
d[S][0] = 0, cnt[S][0] = 1;
priority_queue<Ver, vector<Ver>, greater<Ver>> heap;
heap.push({S, 0, 0});
while(heap.size()){
Ver t = heap.top();
heap.pop();
int ver = t.ver, type = t.type, dis = t.dist, count = cnt[ver][type];
if(st[ver][type]) continue;
st[ver][type] = true;
for(int i = h[ver]; i != -1 ;i = ne[i]){
int j = e[i];
if(d[j][0] > dis + w[i]){
//最短路变为次短路
d[j][1] = d[j][0];
cnt[j][1] = cnt[j][0];
heap.push({j, 1, d[j][1]});
//更新最短路
d[j][0] = dis + w[i];
cnt[j][0] = count;
heap.push({j, 0, d[j][0]});
}
else if(d[j][0] == dis + w[i]){
cnt[j][0] += count;
}else if(d[j][1] > dis + w[i]){
//更新次短路
d[j][1] = dis + w[i];
cnt[j][1] = count;
heap.push({j, 1, d[j][1]});
}else if(d[j][1] == dis + w[i]){
cnt[j][1] += count;
}
}
}
int res = cnt[F][0];
if(d[F][0] + 1 == d[F][1]) res += cnt[F][1];
return res;
}
int main(){
int cases;
cin >> cases;
while(cases--){
memset(h , -1, sizeof h);
idx = 0;
cin >> n >> m ;
for(int i = 0; i < m ; i++ ){
int a,b,c;
cin >> a >> b >> c;
add(a, b, c);
}
cin >> S >> F;
cout << dijkstra() << endl;
}
return 0;
}Floyd算法
最短路


#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 160;
const double INF = 1e20;
int n;
double d[N][N];
PII q[N];
char g[N][N];
double maxd[N];
double get_dist(PII p1, PII p2){
int dx = p1.x - p2.x, dy = p1.y - p2.y;
return sqrt(dx * dx + dy * dy);
}
void floyd(){
for(int k = 0; k < n ; k ++ ){
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
int main()
{
cin >> n;
for(int i = 0 ; i < n ; i ++ ) cin >> q[i].x >> q[i].y;
for(int i = 0 ; i < n ; i ++ ) cin >> g[i];
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++){
if(i != j){
if(g[i][j] == '1') d[i][j] = get_dist(q[i], q[j]);
else d[i][j] = INF;
}
}
}
floyd();
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
if(d[i][j] < INF/ 2){
maxd[i] = max(maxd[i], d[i][j]) ;
}
}
}
double res1 = 0;
for(int i = 0 ; i < n ; i ++ ) res1 = max(res1, maxd[i]);
double res2 = INF;
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
if(d[i][j] >= INF){
res2 = min(res2, maxd[i] + get_dist(q[i], q[j]) + maxd[j]);
}
}
}
printf("%.6lf\n", max(res1, res2));
return 0;
}传递闭包


#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 26;
int n,m;
bool g[N][N], d[N][N];
bool st[N]; //存储当前变量有没有被输出
void floyd(){
memcpy(d, g,sizeof d);
for(int k = 0 ; k < n ; k ++ ){
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < n ; j ++ ){
//若i<k,且k<j,则存在i<j
d[i][j] |= d[i][k] && d[k][j];
}
}
}
}
int check(){
for(int i = 0; i < n ; i ++ ){
if(d[i][i])
//i < i矛盾
return 2;
}
for(int i = 0 ; i < n ; i ++ ){
for(int j = 0 ; j < i ; j ++ ){
// i与j之间没有关系
if(!d[i][j] && !d[j][i]) {
return 0;
}
}
}
return 1;
}
char get_min()
{
for(int i = 0 ; i < n ; i ++ )
{
if(!st[i])
{
bool flag = true;
//找到是否比i小的点
for(int j = 0 ; j < n ; j ++ ){
if(!st[j] && d[j][i]){
flag = false;
break;
}
}
//没有比i小的
if(flag)
{
st[i] = true;
return 'A' + i;
}
}
}
}
int main()
{
while(cin >> n >> m , n || m){
memset(g, 0, sizeof g);
int type = 0; // 0:不确定 1:唯一确定 2:矛盾
int t; //每个结果对应的轮数
for(int i = 1; i <= m ; i ++ ){
char str[5];
cin >> str;
int a = str[0] - 'A', b = str[2] - 'A';
if(!type){
g[a][b] = 1;
floyd();
type = check();
if(type) t = i;
}
}
if(!type) puts("Sorted sequence cannot be determined.");
else if(type == 2) printf("Inconsistency found after %d relations.\n", t);
else{
memset(st, 0, sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for(int i = 0 ; i < n ; i ++ ) cout << get_min(); //每次输出最小值
printf(".\n");
}
}
return 0;
}求最小环
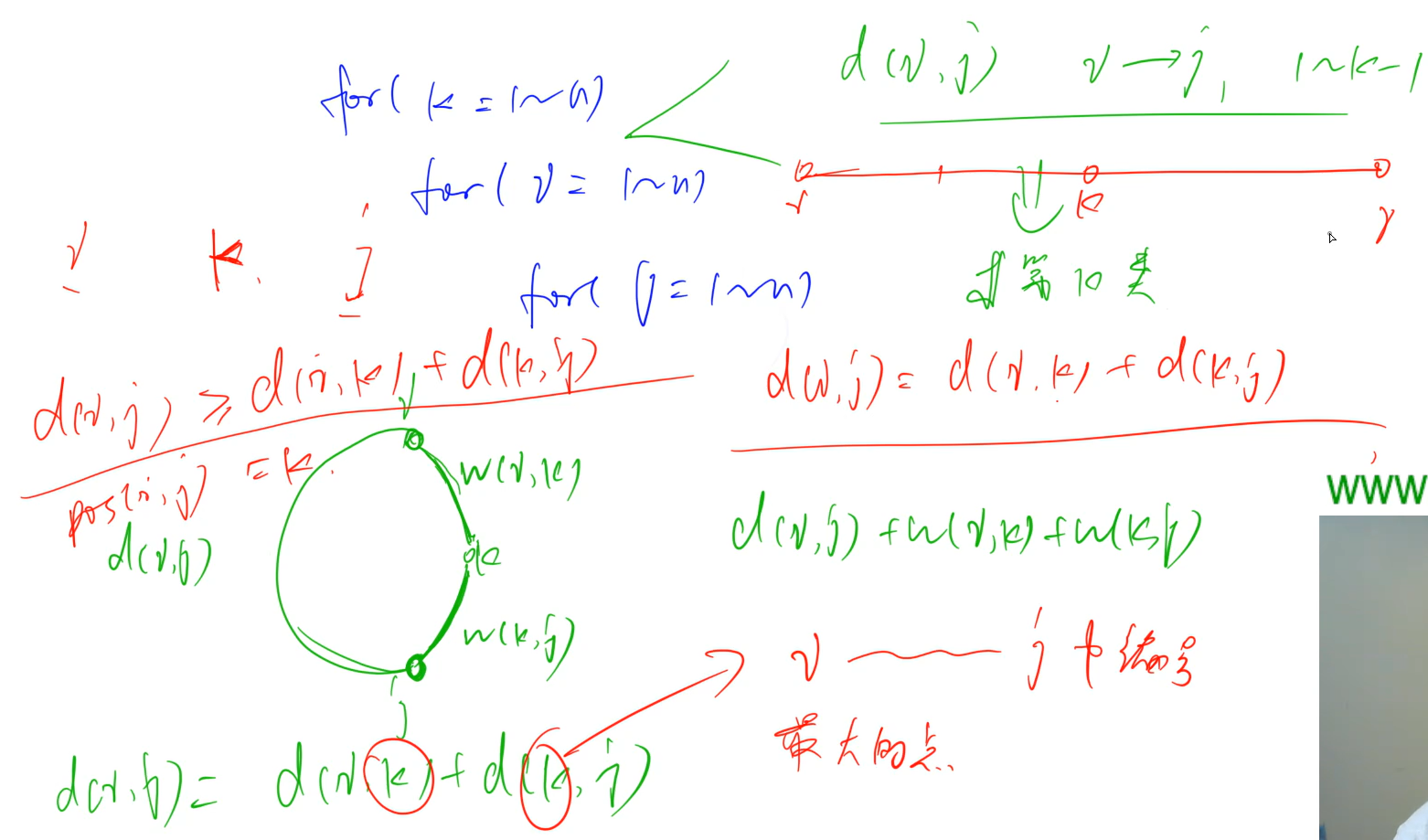
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int d[N][N], g[N][N];
int pos[N][N]; //i到j是由哪个点转移的
int path[N]; //存储路径
int cnt;//路径长度
void get_path(int i,int j){
if(pos[i][j] == 0) return ;
int k = pos[i][j];
get_path(i, k);
path[cnt++] = k;
get_path(k, j);
}
int main()
{
cin >> n >> m ;
memset(g, 0x3f, sizeof g);
for(int i = 0 ; i <= n ; i ++ ) g[i][i] = 0;
for(int i = 0 ; i < m ; i++ ){
int a, b, c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int res = INF;
memcpy(d, g, sizeof d);
for(int k = 1; k <= n ; k ++ ){
for(int i = 1; i <= k ; i ++ ){
for(int j = i + 1 ; j < k ; j ++ ){
if((long long)d[i][j] + g[i][k] + g[k][j] < res) {
res = d[i][j] + g[i][k] + g[k][j];
cnt = 0;
path[cnt++] = k;
path[cnt++] = i;
get_path(i, j);
path[cnt++] = j;
}
}
}
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ; j <= n ; j ++ ){
if(d[i][j] > d[i][k] + d[k][j]){
d[i][j] = d[i][k] + d[k][j];
pos[i][j] = k;
}
}
}
}
if(res > INF / 2) cout << "No solution." << endl;
else {
for(int i = 0 ;i < cnt; i ++ ) cout << path[i] << ' ';
}
return 0;
}

#include <cstring>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
const int N = 210;
int k, n, m, S, E;
int g[N][N];
int res[N][N];
void mul(int c[][N], int a[][N], int b[][N])
{
static int temp[N][N];
memset(temp, 0x3f, sizeof temp);
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]);
memcpy(c, temp, sizeof temp);
}
void qmi()
{
memset(res, 0x3f, sizeof res);
for (int i = 1; i <= n; i ++ ) res[i][i] = 0;
while (k)
{
if (k & 1) mul(res, res, g); // res = res * g
mul(g, g, g); // g = g * g
k >>= 1;
}
}
int main()
{
cin >> k >> m >> S >> E;
memset(g, 0x3f, sizeof g);
map<int, int> ids;
if (!ids.count(S)) ids[S] = ++ n;
if (!ids.count(E)) ids[E] = ++ n;
S = ids[S], E = ids[E];
while (m -- )
{
int a, b, c;
cin >> c >> a >> b;
if (!ids.count(a)) ids[a] = ++ n;
if (!ids.count(b)) ids[b] = ++ n;
a = ids[a], b = ids[b];
g[a][b] = g[b][a] = min(g[a][b], c);
}
qmi();
cout << res[S][E] << endl;
return 0;
}最小生成树
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110,INF = 0x3f3f3f3f;
int n;
int g[N][N];
int d[N];
bool st[N];
int prim()
{
memset(d, 0x3f, sizeof d);
int res = 0;
d[1] = 0;
for(int i = 0 ; i < n ; i ++ )
{
int t = -1;
for(int j = 1 ; j <= n ; j ++ )
{
if(!st[j] &&(t == -1 || d[t] > d[j]))
{
t = j;
}
}
if(i && d[t] == INF) return INF;
if(i) res += d[t];
for(int j = 1 ; j <= n ; j ++ ) d[j] = min(d[j], g[t][j]);
st[t] = true;
}
return res;
}
int main()
{
cin >> n ;
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = 1 ; j <= n ; j ++ )
{
cin >> g[i][j];
}
}
int t = prim();
cout << t << endl;
return 0;
}最小生成森林:只能用kruscal
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110,M = 210, INF = 0x3f3f3f3f;
int n, m;
int p[N];
struct Edge{
int a, b, w;
bool operator <(const Edge &W)const {
return w < W.w;
}
}edges[M];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m ;
int sum = 0;
for(int i = 0 ; i < m ; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
edges[i].a = a, edges[i].b = b, edges[i].w = w;
sum += w;
}
int res = 0, cnt = 0;
sort(edges, edges + m);
for(int i = 1; i <= n ; i ++ ) p[i] = i;
for(int i = 0 ; i < m ; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i]. w;
a = find(a), b = find(b);
if(a != b)
{
p[a] = b;
res += w;
cnt ++ ;
}
}
cout << sum - res << endl;;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 310, M = 8010, INF = 0x3f3f3f3f;
int n, m;
int p[N];
struct Edge{
int a, b, w;
bool operator<(const Edge &W) const {
return w < W.w;
}
}edges[M];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for(int i = 0 ; i < m ; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
edges[i].a = a, edges[i].b = b, edges[i].w = w;
}
for(int i = 1 ; i <= n ; i ++ ) p[i] = i;
sort(edges, edges + m);
int res = 0, cnt = 0, medge = 0 ;
for(int i = 0 ; i < m ; i ++ )
{
int a = edges[i].a ,b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if(a != b){
p[a] = b;
res += w;
medge = max(medge, w);
cnt ++;
}
}
cout << cnt << ' ' << medge << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 2010, M = 10010, INF = 0x3f3f3f3f;
struct Edge
{
int a, b, w;
bool operator<(const Edge&W) const {
return w < W.w;
}
}edges[M];
int n, m;
int p[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for(int i = 1 ; i <= n ; i++ ) p[i] = i;
int res = 0, cnt = 0;
for(int i = 0 ; i < m ; i ++ )
{
int t, a, b, w;
cin >> t >> a >> b >> w;
if(t == 1)
{
p[find(a)] = find(b);
cnt ++ ;
res += w;
}
edges[i].a = a;
edges[i].b = b;
edges[i].w = w;
}
sort(edges , edges + m);
for(int i = 0 ; i < m ; i++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if(a != b){
p[a] = b;
res += w;
cnt ++ ;
}
}
cout << res << endl;
return 0;
}#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010, M = 10010, K = N * N * 2, INF = 0x3f3f3f3f ;
struct Edge{
int a, b, w;
}edges[K];
int n, m, k;
int ids[N][N];
int p[K];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
void get_edges()
{
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}, dw[4] = {1, 2, 1, 2}; //上、右,下,左
for(int z = 0 ; z < 2 ; z ++ )
for(int i = 1; i <= n ; i ++ )
for(int j = 1 ; j <= m ; j ++ )
for(int u = 0 ; u < 4 ; u ++ )
if(u % 2 == z)
{
int x = i + dx[u], y = j + dy[u], w = dw[u];
if(x && x <= n && y && y <= m)
{
int a = ids[i][j], b = ids[x][y];
if(a < b) edges[k ++] = {a, b, w};
}
}
}
int main()
{
cin >> n >> m ;
int t = 1;
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ; j <= m ; j ++ )
{
ids[i][j] = t++;
}
}
for(int i = 1; i <= t ; i ++ ) p[i] = i;
int x1, y1, x2, y2;
while(cin >> x1 >> y1 >> x2 >> y2)
{
int a = ids[x1][y1], b = ids[x2][y2];
p[find(a)] = find(b);
}
get_edges();
int res = 0 ;
for(int i = 0 ; i < k ;i ++ )
{
int a = find(edges[i].a), b = find(edges[i].b), w = edges[i].w;
if(a != b)
{
p[a] = b;
res += w;
}
}
cout << res << endl;
return 0;
}最小生成树的扩展应用
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 310, INF = 0x3f3f3f3f;
int n;
int d[N];
int g[N][N];
bool st[N];
int prim()
{
memset(d, 0x3f, sizeof d);
int res = 0;
for(int i = 0 ; i < n + 1 ; i ++ )
{
int t = -1;
for(int j = 0; j < n + 1 ; j ++ )
if(!st[j] && (t == -1 || d[j] < d[t]))
t = j;
if(i && d[t] == INF) return INF;
if(i) res += d[t];
for(int j = 0 ; j < n + 1; j ++ ) d[j] = min(d[j], g[t][j]);
st[t] = true;
}
return res;
}
int main()
{
cin >> n ;
memset(g, 0x3f, sizeof g);
for(int i = 1; i <= n ; i++ )
{
int a;
cin >> a;
g[0][i] = g[i][0] = a;
}
for(int i = 1; i <= n ; i++ )
for(int j = 1 ; j <= n; j++ )
cin >> g[i][j];
int t = prim();
cout << t << endl;
return 0;
}#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
const int N = 510 , M = N * N / 2;
int n,m,k;
PII q[N];
int p[N];
struct Edge{
int a, b;
double w;
bool operator <(const Edge& W) const {
return w < W.w;
}
}e[M];
double get_dist(PII a, PII b)
{
int dx = a.x - b.x;
int dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
int find(int x)
{
if(p[x] != x) return p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> k;
for(int i = 0 ; i < n ; i++) cin >> q[i].x >> q[i].y;
for(int i = 0 ; i < n ; i ++ )
for(int j = 0 ; j < i ; j ++)
e[m ++ ] = {i , j , get_dist(q[i], q[j])};
sort(e, e + m);
for(int i = 0 ; i < n ; i ++ ) p[i] = i;
int cnt = n;
double res = 0;
for(int i = 0 ; i < m ; i ++ )
{
if(cnt <= k ) break;
int a = find(e[i].a) , b = find(e[i].b);
double w = e[i].w;
if(a != b)
{
p[a] = b;
cnt -- ;
res = w;
}
}
printf("%.2lf\n", res);
return 0;
}
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6010;
struct Edge{
int a, b, w;
bool operator <(const Edge &W) const {
return w < W.w;
}
}e[N];
int n;
int p[N];
int sz[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
int T;
cin >> T;
while(T -- )
{
cin >> n;
for(int i = 0 ; i < n - 1 ; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
e[i] = {a, b, w};
}
sort(e, e + n - 1);
for(int i = 1 ; i <= n ; i ++ ) p[i] = i, sz[i] = 1;
int res = 0;
for(int i = 0 ; i < n - 1 ; i ++ )
{
int a = find(e[i].a), b = find(e[i].b);
int w = e[i].w;
if(a != b)
{
res += (sz[a] * sz[b] - 1) * (w + 1);
sz[b] += sz[a];
p[a] = b;
}
}
cout << res << endl;
}
return 0;
}秘密的牛奶运输(未做)
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 505, M = 10005, L = 10, INF = 2e9;
int n, m, fa[N][L], fMax[N][L][2], f[N];
int dep[N];
LL res = 0, ans = 9e18;
bool st[M];
/*
fMax[i][j][0 / 1] 表示 i 这个点往上跳 2 ^ j 个点,这个范围内的 最大值 / 最小值。
*/
int head[N], numE = 0;
struct Edge{
int next, from, to, dis;
}e[M << 1];
struct E{
int u, v, w;
bool operator < (const E &x) const{
return w < x.w;
}
}g[M];
void inline addEdge(int from, int to, int dis){
e[++numE].next = head[from];
e[numE].to = to;
e[numE].from = from;
e[numE].dis = dis;
head[from] = numE;
}
void dfs(int u, int last){
for(int i = 1; fa[fa[u][i - 1]][i - 1]; i++){
fa[u][i] = fa[fa[u][i - 1]][i - 1];
if(fMax[u][i - 1][0] == fMax[fa[u][i - 1]][i - 1][0]){
fMax[u][i][0] = fMax[u][i - 1][0];
fMax[u][i][1] = max(fMax[u][i - 1][1], fMax[fa[u][i - 1]][i - 1][1]);
}else{
fMax[u][i][0] = max(fMax[u][i - 1][0], fMax[fa[u][i - 1]][i - 1][0]);
fMax[u][i][1] = min(fMax[u][i - 1][0], fMax[fa[u][i - 1]][i - 1][0]);
}
}
for(int i = head[u]; i; i = e[i].next){
int v = e[i].to;
if(v == last) continue;
fa[v][0] = u, fMax[v][0][0] = e[i].dis;
dep[v] = dep[u] + 1, fMax[v][0][1] = -INF;
dfs(v, u);
}
}
int find(int x){
return x == f[x] ? x : f[x] = find(f[x]);
}
void inline update(int v, int &val1, int &val2){
if(v > val1) val2 = val1, val1 = v;
else if(v > val2 && v != val1) val2 = v;
}
void inline lca(int x, int y, int &val1, int &val2){
if(dep[x] < dep[y]) swap(x, y);
for(int i = L - 1; ~i; i--)
if(dep[x] - (1 << i) >= dep[y]) {
update(fMax[x][i][0], val1, val2);
update(fMax[x][i][1], val1, val2);
x = fa[x][i];
}
if(x == y) return;
for(int i = L - 1; ~i; i--){
if(fa[x][i] != fa[y][i]){
update(fMax[x][i][0], val1, val2);
update(fMax[x][i][1], val1, val2);
update(fMax[y][i][0], val1, val2);
update(fMax[y][i][1], val1, val2);
x = fa[x][i], y = fa[y][i];
}
}
update(fMax[x][0][0], val1, val2);
update(fMax[x][0][1], val1, val2);
update(fMax[y][0][0], val1, val2);
update(fMax[y][0][1], val1, val2);
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
f[i] = i;
for(int i = 1; i <= m; i++){
int u, v, w; scanf("%d%d%d", &u, &v, &w);
g[i] = (E){ u, v, w };
}
sort(g + 1, g + 1 + m);
for(int i = 1; i <= m; i++){
int u = find(g[i].u), v = find(g[i].v), w = g[i].w;
if(u != v){
f[u] = v, res += w, st[i] = true;
addEdge(g[i].u, g[i].v, w); addEdge(g[i].v, g[i].u, w);
}
}
dfs(1, 0);
for(int i = 1; i <= m; i++){
if(!st[i]){
int val1 = -INF, val2 = -INF;
lca(g[i].u, g[i].v, val1, val2);
if(val1 == g[i].w)
ans = min(ans, res - val2 + g[i].w);
else ans = min(ans, res - val1 + g[i].w);
}
}
printf("%lld\n", ans);
return 0;
}


