算法（五）动态规划

基础课

DP问题总思想

for 物品
    for 体积
        for 决策

背包问题

我们有一个背包容量是V，有N件物品，每个物品的占用空间是Vi，每个物体的权重（价值）是Wi

01背包

每个物品最多只用一次

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ; j <= m ; j ++ )
            {
                f[i][j] = f[i-1][j];//不包含i时的状态转移
                if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);//当j大于v[i]时，说明能装下，则是包含i的状态转移，这里可以看成先整个去掉i，再加上i
            }
            
    cout << f[n][m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			v[i] = nextInt();
			w[i] = nextInt();
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				f[i][j] = f[i - 1][j];
				if (j >= v[i])
					f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
			}
		}
		out.print(f[n][m]);
		out.flush();
	}
}

一维方法

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;
int f[N];
int v[N],w[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = m ; j >= v[i] ; j -- )
        {
            f[j] = max(f[j], f[j-v[i]] + w[i]);
            //若仍为j++形式，则f[j-v[i]]与f[i][j-v[i]]相同，而这是不对的
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int f[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			v[i] = nextInt();
			w[i] = nextInt();
		}
		for (int i = 1; i <= n; i++) {
			for (int j = m; j >= v[i]; j--) {
				f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
			}
		}
		out.print(f[m]);
		out.flush();
	}
}

完全背包

每个物品有无限个

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;
int f[N][N];
int v[N],w[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= m ; j ++ )
        {
            for(int k = 0 ; k * v[i] <= j ; k ++ )
            {
                f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			v[i] = nextInt();
			w[i] = nextInt();
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				for (int k = 0; k * v[i] <= j; k++) {
					f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
				}
			}
		}
		out.print(f[n][m]);
		out.flush();
	}
}

优化

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;
int f[N][N];
int v[N],w[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= m ; j ++ )
        {
            f[i][j] = f[i-1][j];
            if(j>=v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			v[i] = nextInt();
			w[i] = nextInt();
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				f[i][j] = f[i-1][j];
				if(j >= v[i]) f[i][j] = Math.max(f[i][j], f[i][j-v[i]]+w[i]);
			}
		}
		out.print(f[n][m]);
		out.flush();
	}
}

一维优化

当空间优化到1维时，只有完全背包问题的体积是从小到大的

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;
int f[N];
int v[N],w[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = v[i] ; j <= m ; j ++ )
        {
            f[j] = max(f[j], f[j-v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int f[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			v[i] = nextInt();
			w[i] = nextInt();
		}
		for (int i = 1; i <= n; i++) {
			for (int j = v[i]; j <= m; j++) {
			    f[j] = Math.max(f[j], f[j-v[i]]+w[i]);
			}
		}
		out.print(f[m]);
		out.flush();
	}
}

多重背包

每个物品的数量为Si

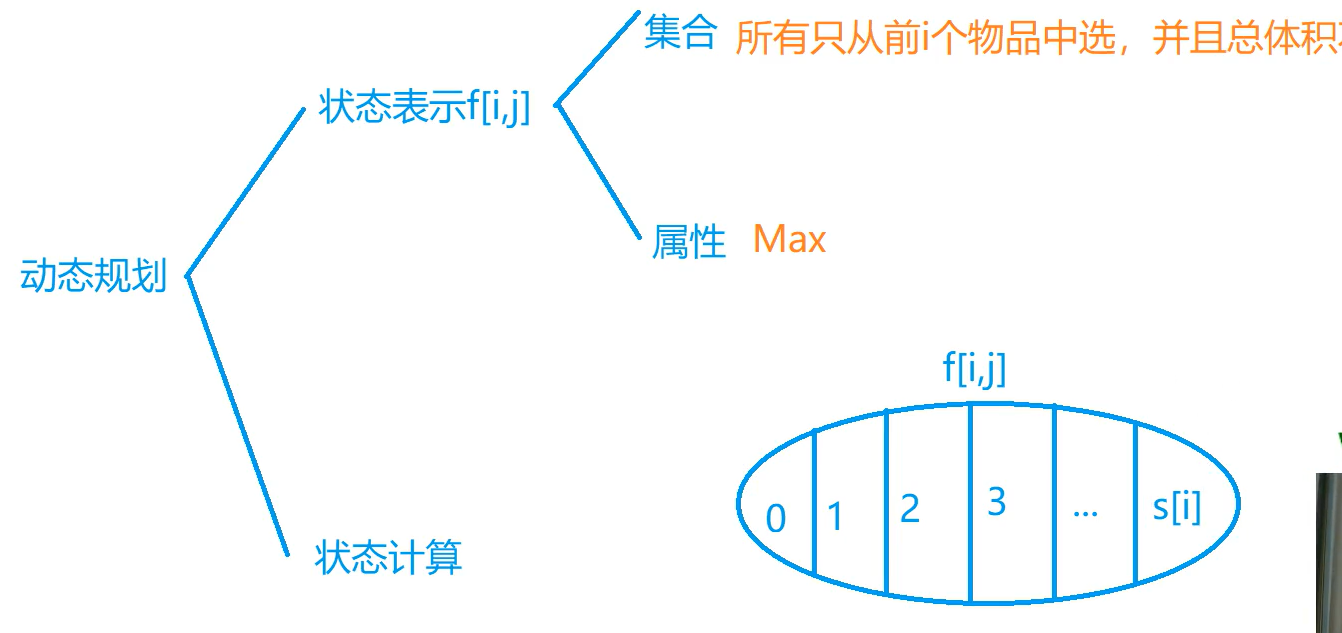
f[i][j] = max(f[i - 1][j - v[i] * k] + w[i] * k)

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 110;

int n,m;
int v[N],w[N],s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= m ; j ++ )
        {
            for(int k = 0 ; k <= s[i] && k*v[i] <= j ; k ++ )
            {
                f[i][j] = max(f[i][j], f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int s[] = new int[N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			v[i] = nextInt();
			w[i] = nextInt();
			s[i] = nextInt();
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				for (int k = 0; k <= s[i] && k * v[i] <= j; k++) {
					f[i][j] = Math.max(f[i][j], f[i-1][j - k * v[i]] + k*w[i]);
				}
			}
		}
		out.print(f[n][m]);
		out.flush();
	}
}

利用二进制进行优化，将NVS时间复杂度优化为NVlogS

如S=200，可拆分成1,2,4,8，…，64,73（73是因为1加到64为127，因此不能再取128）

这样就转化为01背包问题

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 25000; // 2000 * log2000
int n,m;
int v[N],w[N],s[N];
int f[N];

int main()
{
    cin >> n >> m;
    int cnt = 0;
    for(int i = 1; i <= n ; i ++ )
    {
        int a,b,s;
        cin >> a >> b >> s;
        int k = 1;
        while(k<=s)
        {
            cnt ++ ;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0)
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    
    n = cnt ;
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = m ; j >= v[i] ; j -- )
        {
            f[j] = max(f[j] , f[j-v[i]] + w[i]);
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 25000;
	public static int n, m;
	public static int v[] = new int[N];
	public static int w[] = new int[N];
	public static int s[] = new int[N];
	public static int f[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		int cnt = 0;
		for (int i = 1; i <= n; i++) {
			int a, b, s;
			a = nextInt();
			b = nextInt();
			s = nextInt();
			int k = 1;
			while (k <= s) {
				cnt++;
				v[cnt] = a * k;
				w[cnt] = b * k;
				s -= k;
				k *= 2;
			}
			if (s > 0) {
				cnt++;
				v[cnt] = a * s;
				w[cnt] = b * s;
			}
		}
		n = cnt ;
		for (int i = 1; i <= n; i++) {
			for (int j = m; j >= v[i]; j--) {
				f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
			}
		}
		out.print(f[m]);
		out.flush();
	}
}

分组背包

物品会分组，每个组里面只能选一个物品

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 110;

int n,m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ )
    {
        cin >> s[i];
        for(int j = 0 ; j < s[i] ; j ++ )
        {
            cin >> v[i][j] >> w[i][j];
        }
    }
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = m ; j >= 0 ; j -- )
        {
            for(int k = 0 ; k < s[i] ; k ++ ) //枚举从第i个组里选哪个
            {
                if(v[i][k] <= j) f[j] = max(f[j],f[j-v[i][k]] + w[i][k]);
            }
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 110;
	public static int n, m;
	public static int v[][] = new int[N][N];
	public static int w[][] = new int[N][N];
	public static int s[] = new int[N];
	public static int f[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			s[i] = nextInt();
			for (int j = 0; j < s[i]; j++) {
				v[i][j] = nextInt();
				w[i][j] = nextInt();
			}
		}
		for (int i = 1; i <= n; i++) {
			for (int j = m; j >= 0; j--) {
				for (int k = 0; k < s[i]; k++) {
					if (v[i][k] <= j)
						f[j] = Math.max(f[j], f[j - v[i][k]] + w[i][k]);
				}
			}
		}
		out.print(f[m]);
		out.flush();
	}
}

线性dp

数字三角形

#include<iostream>
#include<algorithm>

using namespace std;
const int N = 510, INF = 1e9;
int n,m;
int f[N][N]; //存储状态
int a[N][N]; //存储三角形中的每个点

int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++ ) 
    {
        for(int j = 1 ; j <= i ; j ++ )
        {
            cin >> a[i][j];
        }
    }
    
    for(int i = 0 ; i <= n ; i ++ )
    {
        for(int j = 0 ; j <= i + 1 ; j ++ )
        {
            f[i][j] = -INF;
        }
    }
    
    f[1][1] = a[1][1];
    for(int i = 2 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= i ; j ++ )
        {
            f[i][j] = max(f[i-1][j-1] , f[i-1][j]) + a[i][j];
        }
    }
    int res = -INF;
    for(int i = 1 ; i <= n ; i ++ ) res = max(res,f[n][i]);
    cout << res << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 510, INF = (int) 1e9;
	public static int n;
	public static int a[][] = new int[N][N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= i; j++) {
				a[i][j] = nextInt();
			}
		}
		for (int i = 0; i <= n; i++) {
			for (int j = 0; j <= i + 1; j++) {
				f[i][j] = -INF;
			}
		}
		f[1][1] = a[1][1];
		for (int i = 2; i <= n; i++) {
			for (int j = 1; j <= i; j++) {
				f[i][j] = Math.max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
			}
		}
		int res = -INF;
		for (int i = 1; i <= n; i++) {
			res = Math.max(res, f[n][i]);
		}
		out.print(res);
		out.flush();
	}
}

最长上升子序列

dp问题的时间复杂度：状态数量*计算每个状态需要的时间

#include<iostream>

using namespace std;

const int N = 1010;

int n;
int a[N];
int f[N];

int main()
{
    cin >> n ;
    for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
    for(int i = 1 ; i <= n ; i ++ )
    {
        f[i] = 1; //最坏的情况下也有它本身一个数
        for(int j = 1 ; j < i ; j ++ )
        {
            if(a[j] < a[i])
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }
    int res = 0;
    for(int i = 1 ; i <= n ; i ++ ) res = max(res, f[i]);
    cout << res << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010, INF = (int) 1e9;
	public static int n;
	public static int a[] = new int[N];
	public static int f[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for (int i = 1; i <= n; i++) {
			a[i] = nextInt();
		}

		for (int i = 1; i <= n; i++) {
			f[i] = 1;
			for (int j = 1; j < i; j++) {
				if (a[j] < a[i]) {
					f[i] = Math.max(f[i], f[j] + 1);
				}
			}
		}
		int res = 0;
		for (int i = 1; i <= n; i++)
			res = Math.max(f[i], res);
		out.print(res);
		out.flush();
	}
}

存储最长子序列

#include<iostream>

using namespace std;

const int N = 1010;

int n;
int a[N];
int f[N];
int g[N]; //用于存储某个点的上一个点
int main()
{
    cin >> n ;
    for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
    for(int i = 1 ; i <= n ; i ++ )
    {
        f[i] = 1; 
        for(int j = 1 ; j < i ; j ++ )
        {
            if(a[j] < a[i])
            {
                if(f[j] + 1 > f[i])
                {
                    f[i] = f[j] + 1;
                    g[i] = j;
                }
            }
        }
    }
    int k = 1;
    for(int i = 1 ; i <= n ; i ++ ) 
    {
        if(f[k] < f[i])
        {
            k = i;   
        }
    }
    cout << f[k] << endl;
    for(int i = 0 , len = f[k] ; i < len ; i ++ )
    {
        cout << a[k] << ' ';
        k = g[k];
    }
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010, INF = (int) 1e9;
	public static int n;
	public static int a[] = new int[N];
	public static int f[] = new int[N];
	public static int g[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for (int i = 1; i <= n; i++) {
			a[i] = nextInt();
		}

		for (int i = 1; i <= n; i++) {
			f[i] = 1;
			for (int j = 1; j < i; j++) {
				if (a[j] < a[i]) {
				    if(f[j] + 1 > f[i]) 
					{
					    g[i] = j; 
					    f[i] = f[j] + 1;
					}
				}
			}
		}
		int k = 0;
		for (int i = 1; i <= n; i++)
		{
		    if(f[i] > f[k]){
		        k = i;
		    }
		}
		out.println(f[k]);
		for(int i = 0 , len = f[k] ; i < len ; i ++ ){
		    out.print(a[k] + " ");
		    k = g[k];
		}

		out.flush();
	}
}

最长上升子序列II

数据加强了，n2的时间复杂度太大

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;

int n;
int a[N];
int q[N];

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++ )  cin >> a[i] ;
    
    int len = 0;
    for(int i = 0 ; i < n ; i ++ )
    {
        //二分查找当前序列中小于当前数的最大值
        int l = 0 , r = len;
        while(l < r)
        {
            int mid = l + r + 1 >> 1 ;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    
    cout << len << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 100010;
	public static int n;
	public static int a[] = new int[N];
	public static int q[] = new int[N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for (int i = 0; i < n; i++)
			a[i] = nextInt();
		int len = 0;
		for (int i = 0; i < n; i++) {
			int l = 0, r = len;
			while (l < r) {
				int mid = l + r + 1 >> 1;
				if (q[mid] < a[i])
					l = mid;
				else
					r = mid - 1;
			}

			len = Math.max(len, r + 1);
			q[r + 1] = a[i];
		}
		out.print(len);
		out.flush();
	}
}

最长公共子序列

注意：四种集合中的元素包含重复的情况，但是因为求的是最大值，因此重复也无所谓

#include<iostream>

using namespace std;

const int N = 1010;
int n,m;
char a[N],b[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    cin >> a + 1 >> b + 1;
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= m ;  j ++ )
        {
            f[i][j] = max(f[i-1][j],f[i][j-1]);
            if(a[i] == b[j]) f[i][j] = max(f[i][j],f[i-1][j-1] + 1);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010;
	public static int n,m;
	public static char a[] = new char[N];
	public static char b[] = new char[N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		String str = br.readLine();
		String[] chs = str.split(" ");
		n = Integer.parseInt(chs[0]);
		m = Integer.parseInt(chs[1]);
		str = br.readLine();
		for(int i = 1 ; i <= n; i ++ ) {
			a[i] = str.charAt(i-1);
		}
		str = br.readLine();
		for(int i = 1 ; i <= m; i ++ ) {
			b[i] = str.charAt(i-1);
		}
		for(int i = 1; i <= n; i ++ ) {
			for(int j = 1 ; j <= m; j ++ ) {
				f[i][j] = Math.max(f[i-1][j], f[i][j-1]);
				if(a[i] == b[j]) f[i][j] = Math.max(f[i][j], f[i-1][j-1] + 1);
			}
		}
		out.print(f[n][m]);
		out.flush();
	}
}

区间dp

石子合并

#include<iostream>

using namespace std;

const int N = 310;
int n;
int f[N][N];
int s[N];

int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++ ) cin >> s[i];
    for(int i = 1 ; i <= n ; i ++ ) s[i] += s[i-1];
    
    for(int len = 2; len <= n ; len ++ )
    {
        for(int i = 1 ; i + len - 1 <= n ; i ++ )
        {
            int l = i , r = i + len - 1;
            f[l][r] = 1e8;
            for(int k = l ; k < r ; k ++ )
                f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
        }
    }
    
    cout << f[1][n] << endl;
    return 0;
}

import java.io.*;
import java.util.*;
public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 310;
	public static int n;
	public static int a[] = new int[N];
	public static int s[] = new int[N];
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for(int i = 1 ; i <= n; i ++ ) a[i] = nextInt();
		for(int i = 1 ; i <= n; i ++ ) s[i] = s[i-1] + a[i];
		for(int len = 2 ; len <= n ; len ++ ) {
			for(int i = 1 ; i + len - 1 <= n ; i ++ ) {
				int l = i, r = i + len - 1;
				f[l][r] = (int)1e8;
				for(int k = l;k < r; k ++ ) {
					f[l][r] = Math.min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
				}
			}
		}
		out.print(f[1][n]);
		out.flush();
	}
}

数位统计类dp

计数问题

原题链接：https://www.acwing.com/problem/content/340/

#include<iostream>
#include<cstring>
#include<vector>

using namespace std;

const int N = 10;

int get(vector<int> num,int l,int r) //注：l是高位，r是低位
{
    int res = 0;
    for(int i = l ; i >= r ; i -- ) res = res * 10 + num[i];
    return res;
}

int power10(int x) //得到x^10
{
    int res = 1;
    while(x--) res *= 10;
    return res;
}
//计算1~n上的x的出现位数
int count(int n,int x) 
{
    if(!n) return 0;//若n为0，则肯定为0
    
    vector<int> num;//存储n的每一位
    while(n)
    {
        num.push_back(n%10);
        n/=10;
    }
    
    n = num.size();
    
    int res = 0;
    //若x为0，由于最高位不能是0，因此从倒数第二位n-2开始计数
    for(int i = n - 1 - !x ; i >= 0 ; i -- )
    {
        if(i < n - 1)
        {
            res += get(num,n-1,i+1) * power10(i);
            if(!x) res -= power10(i); //如果x为0时，x的前一位要从1开始记
        }
        
        if(num[i] == x) res += get(num,i-1,0) + 1;
        else if(num[i] > x) res += power10(i);
    }
    
    return res;
}

int main()
{
    int a,b;
    while(cin >> a >> b,a) //a的意思是判断终止条件
    {
        if(a > b) swap(a,b);
        
        for(int i = 0 ; i <= 9 ; i ++ )
        {
            cout << count(b,i) - count(a-1, i) << ' ';
        }
        cout << endl;
    }
    return 0;
}

import java.io.*;
import java.util.*;
public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010, M = (int) 1e9 + 7;
	public static int n;
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		f[0][0] = 1;
		for (int i = 1; i <= n; i++) {
			for (int j = 0; j <= n; j++) {
				for (int k = 0; k * i <= j; k++) {
					f[i][j] += f[i - 1][j - k * i];
					f[i][j] %= M;
				}
			}
		}
		
		out.print(f[n][n]);
		out.flush();
	}
}

import java.io.*;
import java.util.*;
public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 1010, M = (int) 1e9 + 7;
	public static int n;
	public static int f[][] = new int[N][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		f[0][0] = 1;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= i; j++) {
                f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % M;
			}
		}
		int res = 0;
        for(int i=1; i<=n; i++){
            res = (res + f[n][i]) % M;
        }
		out.print(res);
		out.flush();
	}
}

状态压缩DP

蒙德里安的梦想

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const int N = 12 , M = 1 << N;

ll f[N][M];
bool st[M]; // 存储每种状态是否有奇数个连续的0，如果奇数个0是无效状态，如果是偶数个零置为true。
vector<int> state[M];//二维数组记录合法的状态

int n,m;

int main()
{
    while(cin >> n >> m , n || m) //读入n和m，并且不是两个0即合法输入就继续读入
    {
        //第一部分：预处理1
        //枚举所有可能状态，先预处理每列不能有奇数个连续的0
        for(int i = 0 ; i < (1 << n) ; i ++ )
        {
            int cnt = 0;//记录连续的0的个数
            bool isValid = true; // 某种状态没有奇数个连续的0则标记为true
            for(int j = 0 ; j < n ; j ++ ) // 遍历这一列，从上到下
            { 
                if((i >> j) & 1)
                {
                    // i >> j位运算，表示i的二进制数的第j位，&1表示该位是否为1
                    if(cnt & 1)
                    {
                        //这一位为1，看前面连续的0的个数，如果是奇数（cnt &1为真）则该状态不合法
                        isValid = false; break;
                    }
                    
                    cnt = 0; // 既然该位是1，并且前面不是奇数个0（经过上面的if判断），计数器清零。
                    //其实清不清零没有影响
                }
                else cnt ++ ;//否则的话该位还是0，则统计连续0的计数器++。
            }
            if(cnt & 1) isValid = false; //该列最下面的那一段判断一下连续的0的个数
            st[i] = isValid;//状态i是否有奇数个连续的0的情况,输入到数组st中
        }
        
        //第二部分：预处理2
        // 经过上面每种状态 连续0的判断，已经筛掉一些状态。
        //下面来看进一步的判断：看第i-2列伸出来的和第i-1列伸出去的是否冲突
        for(int j = 0 ; j < (1 << n) ; j ++) //枚举i列所有状态
        {
            state[j].clear(); //清空上次操作遗留的状态，防止影响本次状态。
            for(int k = 0 ; k < (1 << n) ; k ++ ){ // 枚举i-1列所有状态
                if((j & k) == 0 && st[j|k]) 
                //(j & k) == 0指的是i-1列的同一行不能既有i-2列插过来的，同时又有本身自己的1
                //j|k指的是i-1列到底有几个1，st[j|k]是看当前的状态是否合法
                    state[j].push_back(k);
            }
        }
        
        //第三部分：dp开始
        memset(f, 0, sizeof f);  
        //全部初始化为0，因为是连续读入，这里是一个清空操作。
        //类似上面的state[j].clear()        
        
        f[0][0] = 1; //初始状态由于没有从-1列插入该列状态，因此第0列只有竖着摆这一种状态
        for(int i = 1 ;i <= m ; i ++ ) //枚举每一列
        {
            for(int j = 0 ; j < (1 << n) ; j++ ) //枚举每种状态
            {
                for(auto k : state[j]) // 遍历上面已经预处理过的i-1列可转移的状态
                    f[i][j] += f[i-1][k]; // 当前列的方案数就等于之前的第i-1列所有状态k的累加。
            }
        }
        
        //f[m][0]表示 前m-1列都处理完，并且第m-1列没有伸出来的所有方案数。
        //即整个棋盘处理完的方案数
        cout << f[m][0] << endl;
    }
    return 0;
}

最短Hamilton路径

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 20 , M = 1 << N; //M是状态压缩的二进制路径

int n;
int w[N][N];
int f[M][N];//所有从0走到j，走过的所有点是i的所有路径

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++ )
    {
        for(int j = 0 ; j < n ; j ++ )
        {
            cin >> w[i][j];
        }
    }
    
    memset(f, 0x3f , sizeof f);
    f[1][0] = 0;
    for(int i = 0 ; i < 1 << n ; i ++ )
    {
        for(int j = 0 ; j  < n ; j ++ )
        {
            if( i >> j & 1 ) //i要包含j的状态才有意义
            {
                for(int k = 0 ; k < n ; k ++ )
                {
                    if((i-(1<<j)) >> k & 1) //若要从k转移到j点，必须在删除j后，包含k点
                    {
                        f[i][j] = min(f[i][j],f[i-(1<<j)][k] + w[k][j]);
                    }
                }
            }
        }
    }
    cout << f[(1<<n) - 1][n-1] << endl;
    return 0;
    
}

import java.io.*;
import java.util.*;

public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 20, M = 1 << N;
	public static int n;
	public static int w[][] = new int[N][N];
	public static int f[][] = new int[M][N];

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				w[i][j] = nextInt();
			}
		}
		for (int i = 0; i < M; i++) {
			Arrays.fill(f[i], 0x3f3f3f3f);
		}
		f[1][0] = 0;
		for (int i = 0; i < 1 << n; i++) {
			for (int j = 0; j < n; j++) {
				if ((i >> j & 1) > 0) {
					for (int k = 0; k < n; k++) {
						if ((((i - (1 << j))) >> k & 1) > 0) {
							f[i][j] = Math.min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
						}
					}
				}
			}
		}
		out.print(f[(1 << n) - 1][n - 1]);
		out.flush();
	}
}

树形dp

没有上司的舞会

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 6010;

int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
bool has_father[N];

void add(int a,int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    f[u][1] = happy[u];
    for(int i = h[u] ; i != -1 ; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        
        f[u][0] += max(f[j][0], f[j][1]); //不选u这个点的方案
        f[u][1] += f[j][0]; // 选u这个点的方案
    }
}

int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++ ) cin >> happy[i];
    memset(h, -1, sizeof h);
    for(int i = 0 ; i < n - 1 ; i ++ )
    {
        int a,b;
        cin >> a >> b ;
        has_father[a] = true;
        add(b,a);
    }
    
    int root = 1;
    while(has_father[root]) root ++ ; //找到根节点
    
    dfs(root);
    
    cout << max(f[root][0],f[root][1]) << endl;
    
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 6010;
	public static int n, idx;
	public static int h[] = new int[N];
	public static int e[] = new int[N];
	public static int ne[] = new int[N];
	public static int happy[] = new int[N];
	public static boolean has_father[] = new boolean[N];
	public static int f[][] = new int[N][2];

	public static void add(int a, int b) {
		e[idx] = b;
		ne[idx] = h[a];
		h[a] = idx++;
	}

	public static void dfs(int u) {
		f[u][1] = happy[u];
		for (int i = h[u]; i != -1; i = ne[i]) {
			int j = e[i];
			dfs(j);

			f[u][0] += Math.max(f[j][0], f[j][1]);
			f[u][1] += f[j][0];
		}
	}

	public static void main(String[] args) throws Exception {
		n = nextInt();
		for (int i = 1; i <= n; i++)
			happy[i] = nextInt();
		Arrays.fill(h, -1);
		for (int i = 0; i < n - 1; i++) {
			int a, b;
			a = nextInt();
			b = nextInt();
			has_father[a] = true;
			add(b, a);
		}

		int root = 1;
		while (has_father[root])
			root++;
		dfs(root);
		out.print(Math.max(f[root][0], f[root][1]));
		out.flush();
	}
}

记忆化搜索

滑雪

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 310;

int n,m;
int h[N][N];
int f[N][N];

int dx[4] = {-1,0,1,0} , dy[4] = {0,1,0,-1};

int dp(int x,int y)
{
    int &v = f[x][y]; //指的是v是个引用，它就代替了f[x][y]
    if(v != -1) return v; //算过了则直接返回
    
    v = 1;
    for(int i = 0 ; i < 4 ; i ++ )
    {
        int a = x + dx[i], b = y + dy[i];
        if(a >= 1 && a <= n && b >= 1 && b <= m && h[a][b] < h[x][y] )
            v = max(v,dp(a,b)+1);
    }
    
    return v;
}

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ; j <= m ; j ++ )
            cin >> h[i][j];
            
    memset(f, -1, sizeof f);
    
    int res = 0;
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ; j <= m ; j ++ )
            res = max(res, dp(i,j));
            
    cout << res << endl;
    return 0;
}

import java.io.*;
import java.util.*;

public class Main {
	public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	public static StreamTokenizer in = new StreamTokenizer(new InputStreamReader(System.in));
	public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

	public static int nextInt() throws Exception {
		in.nextToken();
		return (int) in.nval;
	}

	public static int N = 310;
	public static int n, m;
	public static int h[][] = new int[N][N];
	public static int f[][] = new int[N][N];
	public static int dx[] = { -1, 0, 1, 0 };
	public static int dy[] = { 0, 1, 0, -1 };

	public static int dp(int x, int y) {
		if (f[x][y] != -1)
			return f[x][y];
		f[x][y] = 1;
		for (int i = 0; i < 4; i++) {
			int a = x + dx[i], b = y + dy[i];
			if (a >= 1 && a <= n && b >= 1 && b <= m && h[a][b] < h[x][y]) {
				f[x][y] = Math.max(f[x][y], dp(a, b) + 1);
			}
		}
		return f[x][y];
	}

	public static void main(String[] args) throws Exception {
		n = nextInt();
		m = nextInt();
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				h[i][j] = nextInt();
			}
		}
		
		for(int i = 1 ; i <= n ; i ++ ){
		    Arrays.fill(f[i], -1);
		}
		
		int res = 0;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				res = Math.max(res, dp(i, j));
			}
		}
		out.print(res);
		out.flush();
	}
}

提高课

数字三角形模型

摘花生

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;

int n,m;
int f[N][N];
int w[N][N];

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        cin >> n >> m;
        for(int i = 1 ; i <= n ; i ++ )
            for(int j = 1 ; j <= m ; j ++ )
                cin >> w[i][j];
        
        for(int i = 1 ; i <= n ; i ++ )
            for(int j = 1 ; j <= m ; j ++ )
                f[i][j] = max(f[i-1][j], f[i][j-1]) + w[i][j];
                
        cout << f[n][m] << endl;
    }
    return 0;
}

最低通行费

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110, INF = 1e9;

int n;
int w[N][N];
int f[N][N];

int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ; j <= n ; j ++ )
            cin >> w[i][j];
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ; j <= n ; j ++ )
            if(i == 1 && j == 1) f[i][j] = w[i][j];
            else 
            {
                f[i][j] = INF;
                if(i > 1) f[i][j] = min(f[i][j],f[i-1][j] + w[i][j]);
                if(j > 1) f[i][j] = min(f[i][j],f[i][j-1] + w[i][j]);
            }
    cout << f[n][n] << endl;
    return 0;
}

方格取数

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int w[N][N];
int f[N * 2][N][N];

int main()
{
    scanf("%d", &n);

    int a, b, c;
    while (cin >> a >> b >> c, a || b || c) w[a][b] = c;

    for (int k = 2; k <= n + n; k ++ )
        for (int i1 = 1; i1 <= n; i1 ++ )
            for (int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }

    printf("%d\n", f[n + n][n][n]);
    return 0;
}

最长上升子序列模型

怪盗基德的滑翔翼

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int n;
int f[N];
int a[N];

/*
	正反走各走一遍最长上升子序列
*/
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        cin >> n;
        for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
        
        int res = 0;
        for(int i = 1 ; i <= n ; i ++ )
        {
            f[i] = 1;
            for(int j = 1 ; j < i ; j ++ )
            {
                if(a[i] > a[j])
                    f[i] = max(f[i] , f[j] + 1);
            }
            res = max(res, f[i]);            
        }
        
        for(int i = n ; i ; i -- )
        {
            f[i] = 1;
            for(int j = n ; j > i ; j -- )
            {
                if(a[j] < a[i])
                    f[i] = max(f[i] , f[j] + 1);
            }
            res = max(res, f[i]);            
        }
        cout << res << endl;
    }
    return 0;
}

登山

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 1010;
int n ;
int a[N];
int f[N],g[N];

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++ ) cin >> a[i];
    
    for(int i = 0 ; i < n ; i ++ )
    {
        f[i] = 1;
        for(int j = 0 ; j < n ; j ++ )
        {
            if(a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
        }
    }
    
    for(int i = n - 1; i >= 0; i -- )
    {
        g[i] = 1;
        for(int j = n - 1; j > i ; j -- )
        {
            if(a[j] < a[i])
                g[i] = max(g[i], g[j] + 1);
        }
    }
    
    int res = 0;
    for(int i = 0 ; i < n  ; i ++ )
    {
        res = max(res , f[i] + g[i] - 1);
    }
    
    cout << res << endl;
    return 0;
}

合唱队形

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 110;
int n ;
int a[N];
int f[N],g[N];

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++ ) cin >> a[i];
    
    for(int i = 0 ; i < n ; i ++ )
    {
        f[i] = 1;
        for(int j = 0 ; j < n ; j ++ )
        {
            if(a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
        }
    }
    
    for(int i = n - 1; i >= 0; i -- )
    {
        g[i] = 1;
        for(int j = n - 1; j > i ; j -- )
        {
            if(a[j] < a[i])
                g[i] = max(g[i], g[j] + 1);
        }
    }
    
    int res = 0;
    for(int i = 0 ; i < n  ; i ++ )
    {
        res = max(res , f[i] + g[i] - 1);
    }
    
    cout << n - res << endl;
    return 0;
}

友好城市

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 5010;
typedef  pair<int,int> PII;

int n;
int f[N];
PII a[N];
int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++ ) cin >> a[i].first >> a[i].second;
    
    sort(a,a+n);
    int res = 0;
    for(int i = 0 ; i < n ; i ++ )
    {
        f[i] = 1;
        for(int j = 0 ; j < i ; j ++ )
        {
            if(a[j].second < a[i].second)
            {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        res = max(res, f[i]);
    }
    cout << res << endl;
    return 0;
}

最大上升子序列和

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N];
int f[N];

int main()
{
    cin >> n;
    for(int i = 0 ; i < n ; i ++ ) cin >> a[i];
    int res = 0;
    for(int i = 0 ; i < n ; i ++ )
    {
        f[i] = a[i];
        for(int j = 0 ; j < i ; j ++ )
        {
            if(a[j] < a[i])
            f[i] = max(f[i], f[j] + a[i]);
        }
        
        res = max(res, f[i]);
    }
    
    cout << res << endl;
    return 0;
    
}

拦截导弹

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;

int n;
int q[N];
int f[N], g[N];

int main()
{
    while(cin >> q[n]) n ++ ;
    
    int res = 0;
    for(int i = 0 ; i < n ; i ++ )
    {
        f[i] = 1;
        for(int j = 0 ; j < i ; j ++ )
        {
            if(q[j] >= q[i])
                f[i] = max(f[i], f[j] + 1);
        }
        res = max(res, f[i]);
    }
    cout << res << endl;
    
    int cnt = 0;
    for(int i = 0 ; i < n ; i ++ )
    {
        int k = 0 ;
        while(k < cnt && g[k] < q[i]) k ++ ;
        g[k] = q[i];
        if(k >= cnt) cnt ++ ;
    }
    cout << cnt << endl;
    return 0;
    
    /*
        组一：389 207 155                65
        组二：           300 299 170 158 
}

导弹防御系统

1、用全局最优解并不断更新的方式得到最小值

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 55;
int n;
int h[N];
int up[N],down[N]; //up[N]存储的是每个上升子序列的结尾数，其本身是递减的，down[N]同理
int res;
//dfs参数：u为枚举的当前数，su为上升子序列个数，sd为下降子序列个数
void dfs(int u, int su, int sd)
{
    if(su + sd >= res ) return ;
    if(u == n)
    {
        res = min(res , su + sd);
        return;
    }
    
    int k = 0;
    while(k < su && up[k] >= h[u]) k ++ ;
    if(k < su)
    {
        int t = up[k];
        up[k] = h[u];
        dfs(u+1, su, sd);
        up[k] = t;
    }
    else 
    {
        up[k] = h[u];
        dfs(u+1, su+1, sd);
    }
    
    k = 0;
    while(k < sd && down[k] <= h[u]) k ++ ;
    if(k < sd)
    {
        int t = down[k];
        down[k] = h[u];
        dfs(u+1, su, sd);
        down[k] = t;
    }
    else 
    {
        down[k] = h[u];
        dfs(u+1, su, sd+1);
    }
}

int main()
{
    while(cin >> n , n)
    {
        for(int i = 0 ; i < n ; i ++ ) cin >> h[i];
        
        res = n;
        dfs(0,0,0);
        cout << res << endl;
    }
    
    return 0;
}

2、迭代加深的方式得到最小值（有点没懂）

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 60;

int n;
int h[N];
int up[N], down[N];

bool dfs(int depth, int u, int su, int sd)
{
    if (su + sd > depth) return false;
    if (u == n) return true;

    // 枚举放到上升子序列中的情况
    bool flag = false;
    for (int i = 1; i <= su; i ++ )
        if (up[i] < h[u])
        {
            int t = up[i];
            up[i] = h[u];
            if (dfs(depth, u + 1, su, sd)) return true;
            up[i] = t;
            flag = true;
            break;
        }
    if (!flag)
    {
        up[su + 1] = h[u];
        if (dfs(depth, u + 1, su + 1, sd)) return true;
    }

    // 枚举放到下降子序列中的情况
    flag = false;
    for (int i = 1; i <= sd; i ++ )
        if (down[i] > h[u])
        {
            int t = down[i];
            down[i] = h[u];
            if (dfs(depth, u + 1, su, sd)) return true;
            down[i] = t;
            flag = true;
            break;
        }
    if (!flag)
    {
        down[sd + 1] = h[u];
        if (dfs(depth, u + 1, su, sd + 1)) return true;
    }

    return false;
}

int main()
{
    while (cin >> n, n)
    {
        for (int i = 0; i < n; i ++ ) cin >> h[i];

        int depth = 0;
        while (!dfs(depth, 0, 0, 0)) depth ++ ;

        cout << depth << endl;
    }

    return 0;
}

最长公共上升子序列

不加优化的n^3做法

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];
int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
    for(int i = 1 ; i <= n ; i ++ ) cin >> b[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        for(int j = 1 ; j <= n ; j ++ )
        {
            f[i][j] = f[i-1][j];
            if(a[i] == b[j])
            {
                f[i][j] = max(f[i][j], 1);
                for(int k = 1 ; k < j ; k ++ )
                {
                    if(b[k] < b[j])
                        f[i][j] = max(f[i][j],f[i-1][k] + 1);
                }
            }
        }
    }
    int res = 0;
    for(int i = 1 ; i <= n ; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;
    return 0;
}

加优化的做法

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];
int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
    for(int i = 1 ; i <= n ; i ++ ) cin >> b[i];
    
    for(int i = 1 ; i <= n ; i ++ )
    {
        int maxv = 1;
        for(int j = 1 ; j <= n ; j ++ )
        {
            f[i][j] = f[i-1][j];
            if(a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if(b[j] < a[i]) maxv = max(maxv, f[i][j] + 1);
        }
    }
    int res = 0;
    for(int i = 1 ; i <= n ; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;
    return 0;
}

背包模型

多重背包

庆功会

#include<iostream>
using namespace std;
const int N = 6010;
int n,m;
int f[N];
int main()
{
    cin >> n >> m;
    for(int i = 0 ; i < n ; i ++ )
    {
        int v,w,s;
        cin >> v >> w >> s;
        for(int j = m ; j >= v ; j -- )
        {
            for(int k = 0 ; k <= s && k * v <= j ; k ++ )
            {
                f[j] = max(f[j], f[j-k*v] + k*w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

多重背包III

多重背包问题III

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 20010;

int n,m;
int f[N],g[N],q[N];

int main()
{
    cin >> n >> m; //物品、背包
    for(int i = 0 ; i < n ; i ++)
    {
        int v,w,s;
        cin >> v >> w >> s;
        memcpy(g , f ,sizeof f);
        for(int j = 0 ; j < v ; j ++ ) //枚举余数r
        {
            int hh = 0 , tt = -1;
            for(int k = j ; k <= m ; k += v) // 枚举 r+?*v
            {
                // 去掉超出滑动窗口范围的元素
                if (hh <= tt && q[hh] < k - s*v) hh ++;
                
                //去掉单调队列末尾比当前元素小的, 根据两个元素相对j的位置算偏移量
                //同一窗口内, j, j+v, j+2v后面加的w数量依次递减，所以距离j越远，相对减去的w倍数越大
                while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt --;
        
                q[ ++ tt] = k;  // 把当前元素下标插入单调队列
        
                //计算f[k], max左边为不选,右边为单调队列最大值,加上相对k的偏移量
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);  
            }
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

01背包

采药

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 1010;

int n,m;
int f[N];

int main()
{
    cin >> m >> n;
    for(int i = 0 ; i < n ; i ++ ) //遍历物品
    {
        int v,w;
        cin >> v >> w;
        for(int j = m ; j >= v ; j -- ) //遍历背包
        {
            f[j] = max(f[j], f[j-v] + w);
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

装箱问题

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 20010;
int n,m;
int f[N];
int main()
{
    cin >> m >> n;
    for(int i = 0 ; i < n ;  i ++ )
    {
        int v;
        cin >> v;
        for(int j = m ; j >= v ; j -- )
        {
            f[j] = max(f[j], f[j-v] + v);
        }
    }
    cout << m - f[m] <<endl;
    return 0;
}

开心的金明

#include<iostream>
using namespace std;
const int N = 30010;
int n,m;
int f[N];
int main()
{
    cin >> m >> n;
    for(int i = 1 ; i <= n ; i ++ )
    {
        int v, q;
        cin >> v >> q;
        q *= v;
        for(int j = m ; j >= v ; j -- )
        {
            f[j] = max(f[j], f[j-v] + q);
        }
    }
    cout << f[m] << endl;
    return 0;
}

与贪心结合

能量石

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 10010;

int n;
struct Stone
{
    int s, e, l;
    bool operator <(const Stone &W) const 
    {
        return s * W.l < l * W.s ;
    }
}stone[N];
int f[N];

int main()
{
    int T;
    cin >> T;
    for(int C = 1; C <= T ; C ++ )
    {
        int m = 0;
        cin >> n;
        for(int i = 0 ; i < n ; i ++ )
        {
            int s,e,l;
            cin >> s >> e >> l;
            stone[i] = {s,e,l};
            m += s;
        }
        
        sort(stone,stone + n);
        
        memset(f, -0x3f ,sizeof f);
        f[0] = 0;
        
        for(int i = 0 ; i < n ; i ++)
        {
            int s = stone[i].s, e = stone[i].e, l = stone[i].l;
            for(int j = m ; j >= s ; j -- )
            {
                f[j] = max(f[j], f[j-s] + e - (j - s) * l); 
            }
        }
        
        int res = 0;
        for(int i = 0 ; i <= m ;i ++ ) res = max(res, f[i]);
        printf("Case #%d: %d\n", C ,res);
    }
    
    return 0;
}

求方案数

背包问题求方案数

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n,m;
int f[N]; //体积为j的背包价值最大
int g[N]; //f[j]取最大值的时候的方案数

int main()
{
    cin >> n >> m;
    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    g[0] = 1;
    
    for(int i = 0 ; i < n ; i ++ )
    {
        int v,w;
        cin >> v >> w;
        for(int j = m ; j >= v ; j -- )
        {
            int maxv = max(f[j], f[j - v] + w);
            int cnt  = 0 ;
            if(maxv == f[j]) cnt += g[j];
            if(maxv == f[j-v]+w) cnt += g[j - v];
            g[j] = cnt % mod;
            f[j] = maxv;
        }
    }
    
    int res = 0;
    for(int i = 0 ; i <= m ; i ++ ) res = max(res, f[i]);
    int cnt = 0 ;
    for(int i = 0 ; i <= m ; i ++ )
        if(res == f[i]) //每种最优选法的方案数都应包含在内
            cnt = (cnt + g[i]) % mod;
            
    cout << cnt << endl;
    return 0;
}

数字组合

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 10010;

int n,m;
int f[N];
int main()
{
    cin >> n >> m ;
    f[0] = 1;
    for(int i = 0 ; i < n ; i ++ )
    {
        int a;
        cin >> a;
        for(int j = m ; j >= a ; j -- )
        {
            f[j] += f[j-a];
        }
    }
    cout << f[m] << endl;
    return 0;
}

货币系统1021

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 3010;

int n,m;
int f[N];

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for(int i = 0 ; i < n ; i ++ )
    {
        int v;
        cin >> v;
        for(int j = v ; j <= m ; j ++ )
        {
            f[j] += f[j - v];
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

货币系统532

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110, M = 25010;
int n;
int a[N];
int f[M];

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        int n;
        cin >> n;
        for(int i = 0 ;i < n; i ++) cin >> a[i];
        sort(a, a+n);
        
        int m = a[n-1];
        memset(f, 0, sizeof f);
        f[0] = 1;
        
        int res = 0;
        for(int i = 0 ; i < n ; i ++ )
        {
            if(!f[a[i]]) res ++ ; //当方案数为0的时候，说明不能由前面的面值组成
            for(int j = a[i]; j <= m ; j ++ )
                f[j] += f[j - a[i]];
        }
        
        cout << res << endl;
    }
    return 0;
}

求具体方案

背包问题求具体方案

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = n; i >= 1; i -- )
        for (int j = 0; j <= m; j ++ )
        {
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }

    int j = m;
    for (int i = 1; i <= n; i ++ )
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
        {
            cout << i << ' ';
            j -= v[i];
        }

    return 0;
}

二维费用背包

二维费用的背包问题

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int n,M,V;
int f[N][N];
int main()
{
    cin >> n >> V >> M;
    for(int i = 0 ; i < n ; i ++ )
    {
        int v,m,w;
        cin >> v >> m >> w;
        for(int j = V ; j >= v ; j -- )
        {
            for(int k = M ; k >= m ; k -- )
            {
                f[j][k] = max(f[j][k], f[j-v][k-m] + w);
            }
        }
    }
    cout << f[V][M] << endl;
    return 0;
}

宠物小精灵之收服

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010, M = 510;
int n,V1,V2;
int f[N][M];

int main()
{
    cin >> V1 >> V2 >> n; // 背包1 、背包2 、物品
    for(int i = 0 ; i < n ; i ++ )
    {
        int v1, v2;
        cin >> v1 >> v2;
        for(int j = V1 ; j >= v1 ; j -- )
        {
            for(int k = V2 - 1 ; k >= v2 ; k -- ) //V2 - 1是因为体力不能为0
            {
                f[j][k] = max(f[j][k], f[j - v1][k - v2] + 1);
            }
        }
    }
    
    cout << f[V1][V2 - 1] << ' '; 
    int k = V2 - 1;
    while(k > 0 && f[V1][k-1] == f[V1][V2-1]) k -- ;
    cout << V2 - k << endl;
    return 0;
}

完全背包

求方案数

买书

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int v[4] = {10,20,50,100};
int m;
int f[N];
int main()
{
    cin >> m;
    f[0] = 1;
    for(int i = 0 ; i < 4 ;  i ++ )
    {
        for(int j = 0 ; j <= m ; j ++ )
        {
            if(j>=v[i]) f[j] += f[j-v[i]];
        }
    }
    cout << f[m] << endl;
    return 0;
}

特殊：至少

潜水员

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 22 , M = 80;
int n,m,K;
int f[N][M];
int main()
{
    cin >> n >> m >> K;
    memset(f,0x3f,sizeof f);
    f[0][0] = 0;
    while(K--)
    {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for(int j = n ; j >= 0 ; j -- )
        {
            for(int k = m ; k >= 0 ; k -- )
            {
                f[j][k] = min(f[j][k], f[max(0, j - v1)][max(0, k - v2)] + w);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

分组背包

求方案数

机器分配

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 11 , M = 16;
int n,m;
int w[N][M];
int f[N][M];
int way[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n ; i ++ )
        for(int j = 1 ; j <= m ; j ++ ) 
            cin >> w[i][j] ;
            
            
    for(int i = 1 ; i <= n ; i ++ ) //遍历每组
    {
        for(int j = 1 ; j <= m ; j ++ )
        {
            for(int k = 0 ; k <= j ; k ++ ) //遍历每组设备数
                f[i][j] = max(f[i][j], f[i-1][j-k] + w[i][k]);
        }
    }
    
    cout << f[n][m] << endl;
    
    int j = m;
    for(int i = n ; i ; i -- )
    {
        for(int k = 0 ; k <= j ; k ++ )
        {
            if(f[i][j] == f[i-1][j-k] + w[i][k])
            {
                way[i] = k;
                j -= k;
                break; //因为每个组（公司）只会有一种情况，所以直接break
            }
        }
    }
    
    for(int i = 1 ; i <= n ; i ++ ) cout << i <<  ' ' << way[i] << endl;
    return 0;
}

状态压缩

金明的预算方案

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

const int N = 65, M = 32010;
typedef pair<int,int> PII;
PII master[N]; //主件
vector<PII> servent[N]; //附件
int n,m;
int f[M];
int main()
{
    cin >> m >> n;
    for(int i = 1 ; i <= n ; i ++ )
    {
        int v,p,q;
        cin >> v >> p >> q;
        p*=v; //价格*重要度
        if(!q) master[i] = {v,p};
        else servent[q].push_back({v,p});
    }
    
    for(int i = 1 ; i <= n ; i ++ ) //遍历物品
    {
        for(int u = m ; u >= 0 ; u -= 10 ) //遍历背包（金钱）
        {
            //制做分组背包问题某类里每一个可选择的单元————打包
            //for循环里的servent[i].size()筛选了只有主件会进入循环，附件不能进入
            //二进制枚举物品组内的所有打包单元的状态，共2的n次方种，用j表示每一种，j的第k位1/0表示第k个附件选/不选
            for(int j = 0 ; j < 1 << servent[i].size() ; j ++ )
            {
                //当前这个打包单元的体积是v， 价值是w ，下面这几行代码就是在计算v和w
                int v = master[i].first, w = master[i].second; // 主件必选
                for(int k = 0 ; k < servent[i].size() ; k ++ ) //枚举状态j的每一位
                    if(j >> k & 1) //如果j的第k位是i，说明包含第k个组件
                    {
                        v += servent[i][k].first;
                        w += servent[i][k].second;
                    }
                    
                //已经计算出v和w，做分组背包问题的状态计算
                if(u >= v) f[u] = max(f[u], f[u - v] + w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

混合背包

混合背包问题

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010;

int n,m;
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 0  ; i < n ; i ++ )
    {
        int v, w, s;
        cin >> v >> w >> s;
        if(s == 0) //完全背包
        {
            for(int j = v ; j <= m ; j ++ ) f[j] = max(f[j], f[j - v] + w);
        }
        else 
        {
            if(s == -1) s = 1; //将01背包看成多重背包
            for(int k = 1 ; k <= s ; k *= 2)
            {
                for(int j = m; j >= k * v ; j -- )
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            if(s)
            {
                for(int j = m ; j >= s * v ; j -- )
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

有依赖的背包问题

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int n,m;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    for(int i = h[u]; ~i ; i = ne[i]) //循环物品组
    {
        int son = e[i];
        dfs(e[i]);
        //遍历背包的容积，因为我们是要遍历其子节点，所以当前节点我们是默认选择的。
        //分组背包，当前节点看成分组背包中的一个组，子节点的每种选择看成组内的一种物品
        //我们每一次都默认选择当前结点，因为到最后根节点是必选的。 
        for(int j = m - v[u]; j >= 0 ; j -- ) //循环体积
            for(int k = 0 ; k <= j ; k ++ ) //循环决策
                f[u][j] = max(f[u][j], f[u][j-k] + f[son][k]);
    }
    
    //加上刚刚默认选择的父节点价值
    for(int i = m  ; i >= v[u] ; i -- )
    {
        f[u][i] = f[u][i-v[u]] + w[u];
    }
    
    //因为我们是从叶子结点开始往上做，所以如果背包容积不如当前物品的体积大，那就不能选择当前结点及其子节点，因此赋值为零 
    for(int i = 0 ; i < v[u] ; i ++ )
    {
        f[u][i] = 0;
    }
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    int root;
    for(int i = 1 ; i <= n ; i ++ )
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if(p == -1) root = i;
        else add(p, i);
    }
    
    dfs(root);
    
    cout << f[root][m] << endl;
    return 0;
}